統計

使用者指南的此章節涵蓋數學運算式中可用的核心統計函數。

描述性統計

describe 函數會傳回數值陣列的描述性統計。describe 函數會傳回包含描述性統計的單一元組，其中包含名稱/值組。

以下是一個簡單的範例，從 logs 集合中選取文件的隨機樣本，向量化結果集中的 response_d 欄位，並使用 describe 函數傳回有關向量的描述性統計。

let(a=random(logs, q="*:*", fl="response_d", rows="50000"),
    b=col(a, response_d),
    c=describe(b))

當此運算式傳送至 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "sumsq": 36674200601.78738,
        "max": 1068.854686837548,
        "var": 1957.9752647562789,
        "geometricMean": 854.1445499569674,
        "sum": 42764648.83319176,
        "kurtosis": 0.013189848821424377,
        "N": 50000,
        "min": 656.023249311864,
        "mean": 855.2929766638425,
        "popVar": 1957.936105250984,
        "skewness": 0.0014560741802307174,
        "stdev": 44.24901428005237
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 430
      }
    ]
  }
}

請注意，隨機樣本包含 50,000 個記錄，且回應時間僅為 430 毫秒。此大小的樣本可用於以亞秒級效能可靠地估計非常大的基礎資料集的統計資料。

describe 函數也可以在 Zeppelin-Solr 的表格中視覺化

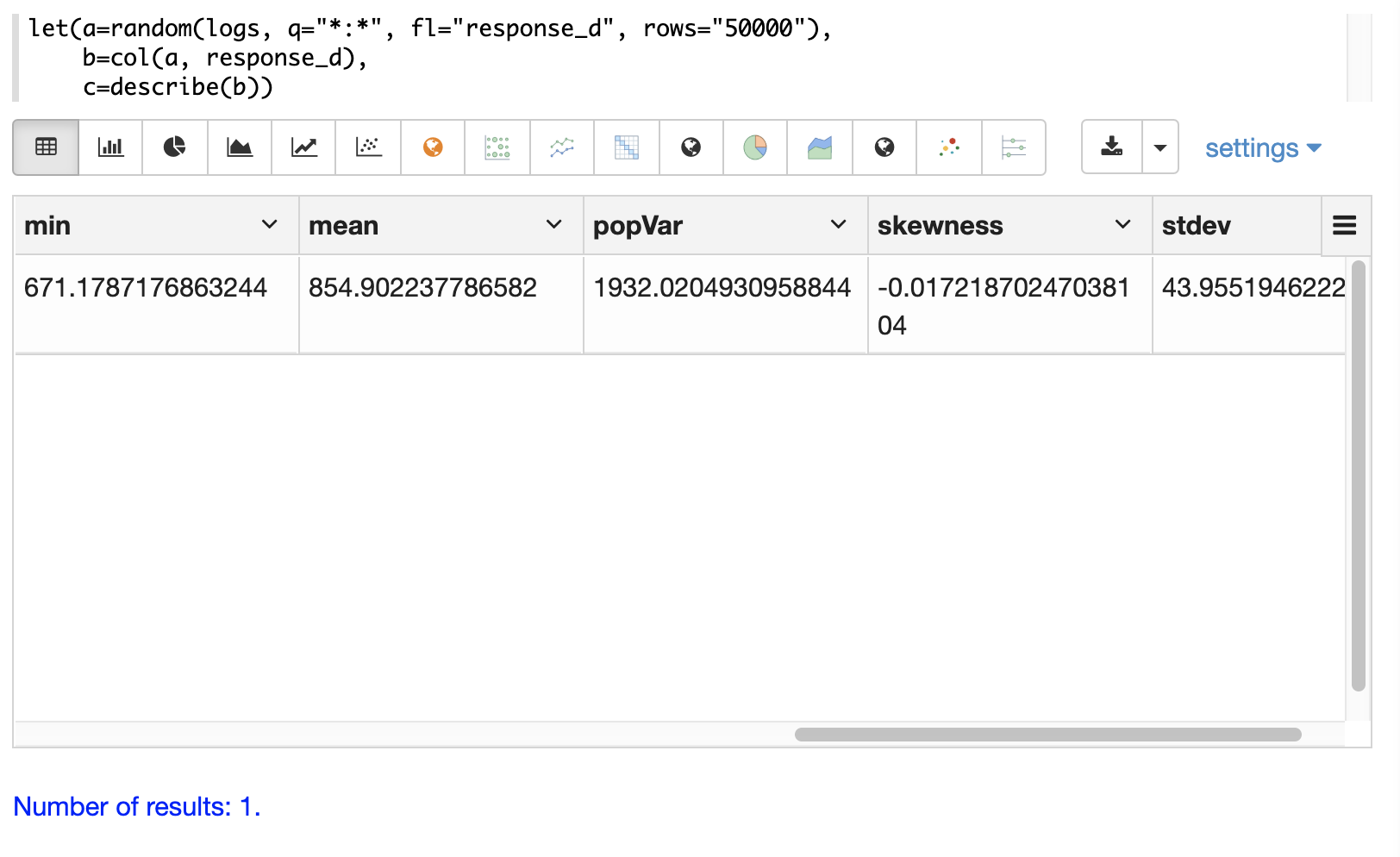
describe

直方圖和頻率表

直方圖和頻率表是視覺化隨機變數分布的工具。

hist 函數會建立一個設計用於連續資料的直方圖。freqTable 函數會建立一個用於離散資料的頻率表。

直方圖

在以下範例中，直方圖用於視覺化來自 logs 集合的回應時間的隨機樣本。此範例使用 random 函數擷取隨機樣本，並從結果集中的 response_d 欄位建立向量。然後將 hist 函數套用至向量，以傳回具有 22 個 bin 的直方圖。hist 函數會傳回一個元組清單，其中包含每個 bin 的摘要統計資訊。

let(a=random(logs, q="*:*", fl="response_d", rows="50000"),
    b=col(a, response_d),
    c=hist(b,  22))

當此運算式傳送至 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "prob": 0.00004896007228311655,
        "min": 675.573084576817,
        "max": 688.3309631697003,
        "mean": 683.805542728906,
        "var": 50.9974629924082,
        "cumProb": 0.000030022417162809913,
        "sum": 2051.416628186718,
        "stdev": 7.141250800273591,
        "N": 3
      },
      {
        "prob": 0.00029607514624062624,
        "min": 696.2875238591652,
        "max": 707.9706315779541,
        "mean": 702.1110569558929,
        "var": 14.136444379466969,
        "cumProb": 0.00022705264963879807,
        "sum": 11233.776911294284,
        "stdev": 3.759846323916307,
        "N": 16
      },
      {
        "prob": 0.0011491235433157194,
        "min": 709.1574910598678,
        "max": 724.9027194369135,
        "mean": 717.8554290699951,
        "var": 20.6935845290122,
        "cumProb": 0.0009858515418689757,
        "sum": 41635.61488605971,
        "stdev": 4.549020172412098,
        "N": 58
      },
      ...
      ]}}

使用 Zeppelin-Solr，直方圖可以先視覺化為表格

histtable

接著，可以利用面積圖將直方圖視覺化，方法是將 x 軸繪製為組距的 平均值，並將 y 軸繪製為 prob (機率)。

hist

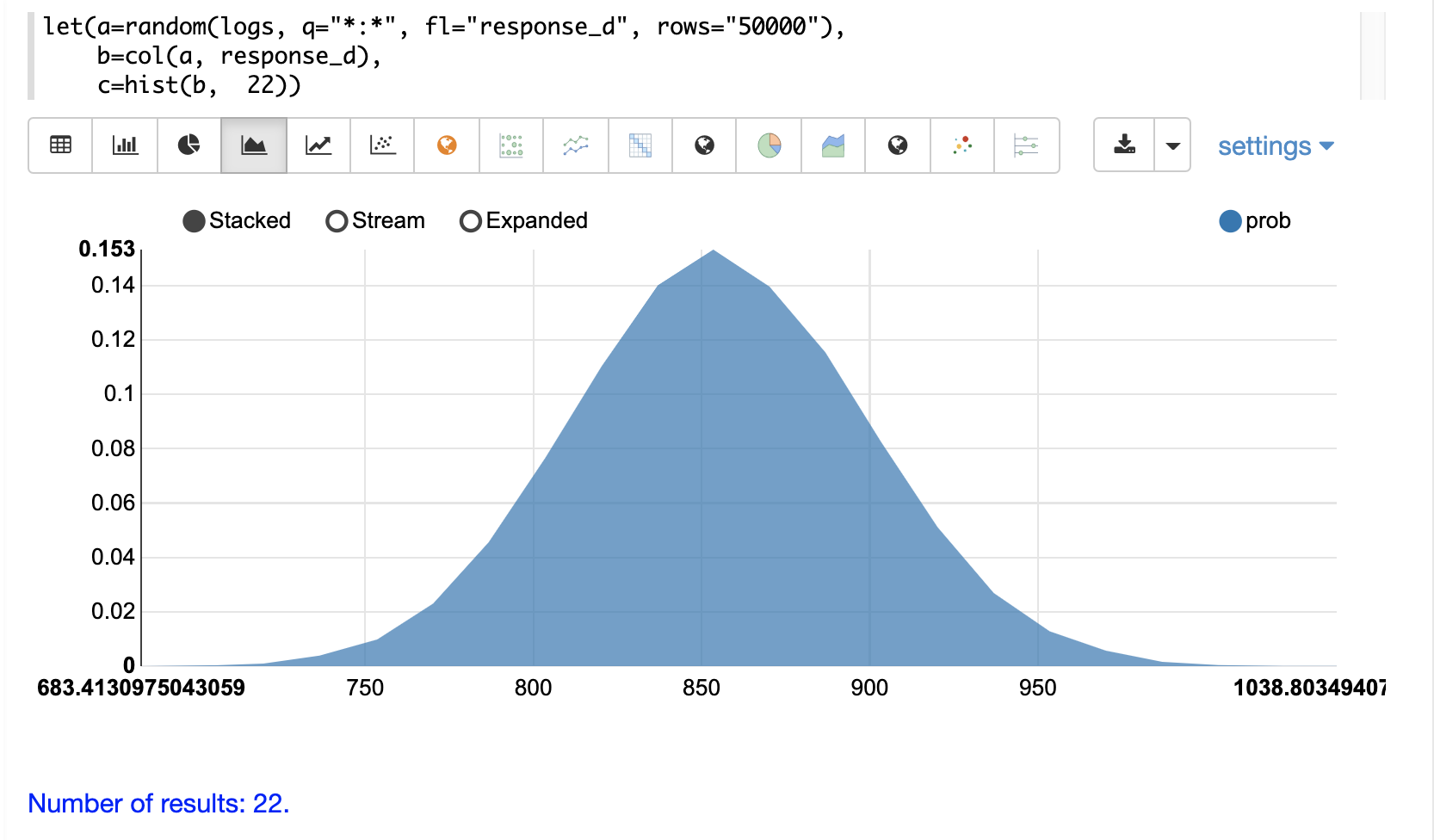
透過將 y 軸切換為 cumProb 欄位，可以繪製累積機率。

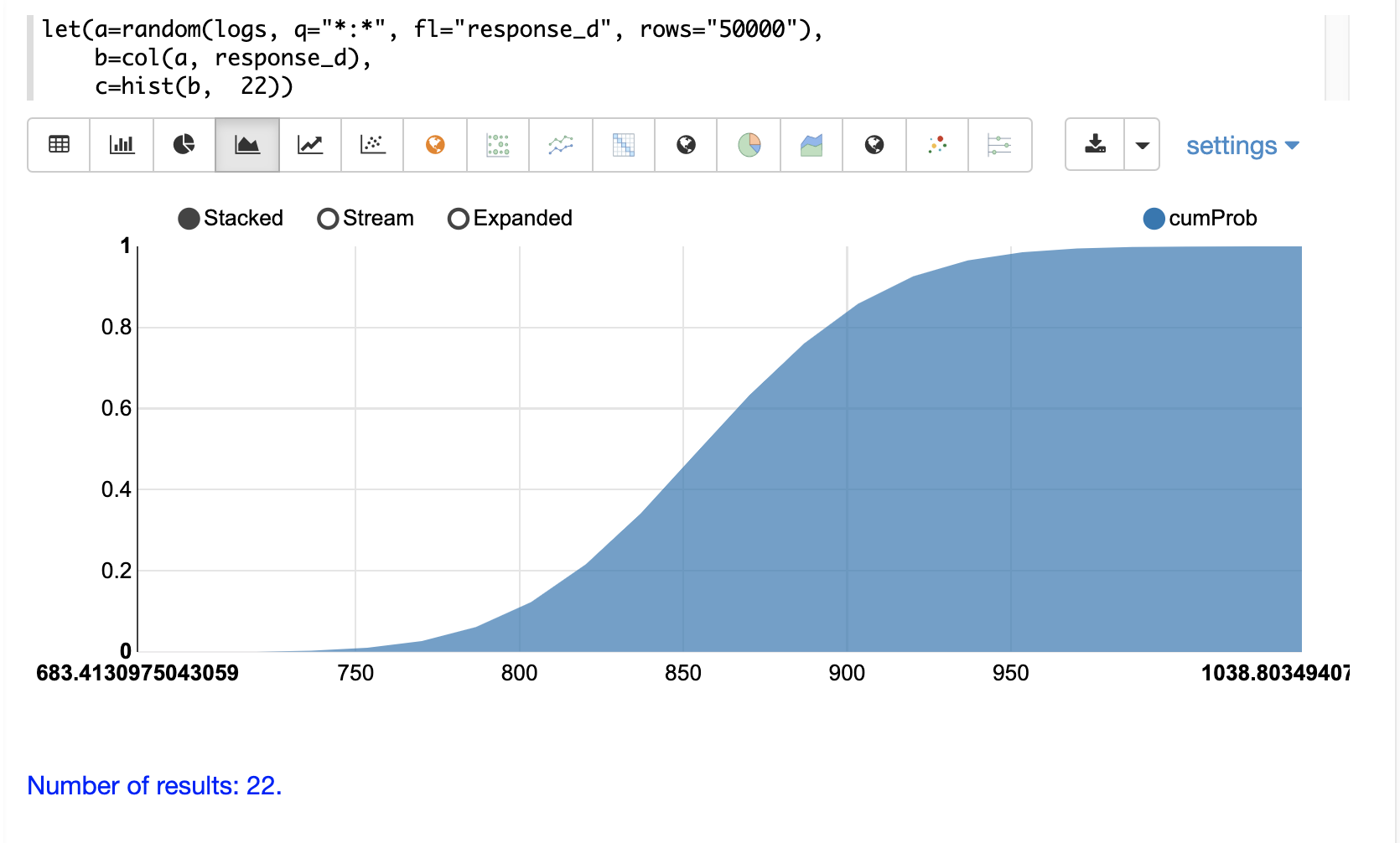
cumProb

自訂直方圖

可以透過將多個 stats 函數的輸出組合到單一直方圖中來定義和視覺化自訂直方圖。自訂直方圖允許基於查詢比較組距，而不是自動對數值欄位進行分組。

stats 函數首先在使用者指南的「搜尋、取樣和彙總」章節中討論。

一個簡單的範例將說明如何定義和視覺化自訂直方圖。

在此範例中，三個 stats 函數被包裝在一個 plist 函數中。plist (平行列表) 函數平行執行其每個內部函數，並將結果串連成單一資料流。plist 還會維護每個子函數輸出的順序。在此範例中，每個 stats 函數都會計算符合特定查詢的文件計數。在此情況下，它們會計算包含 copper、gold 和 silver 等詞彙的文件數量。然後，包含計數的元組列表會儲存在變數 a 中。

接著，建立標籤的 array 並設定為變數 l。

最後，使用 zplot 函數繪製標籤向量和 count(*) 欄位。請注意，col 函數在 zplot 函數內部使用，以從 stats 結果中提取計數。

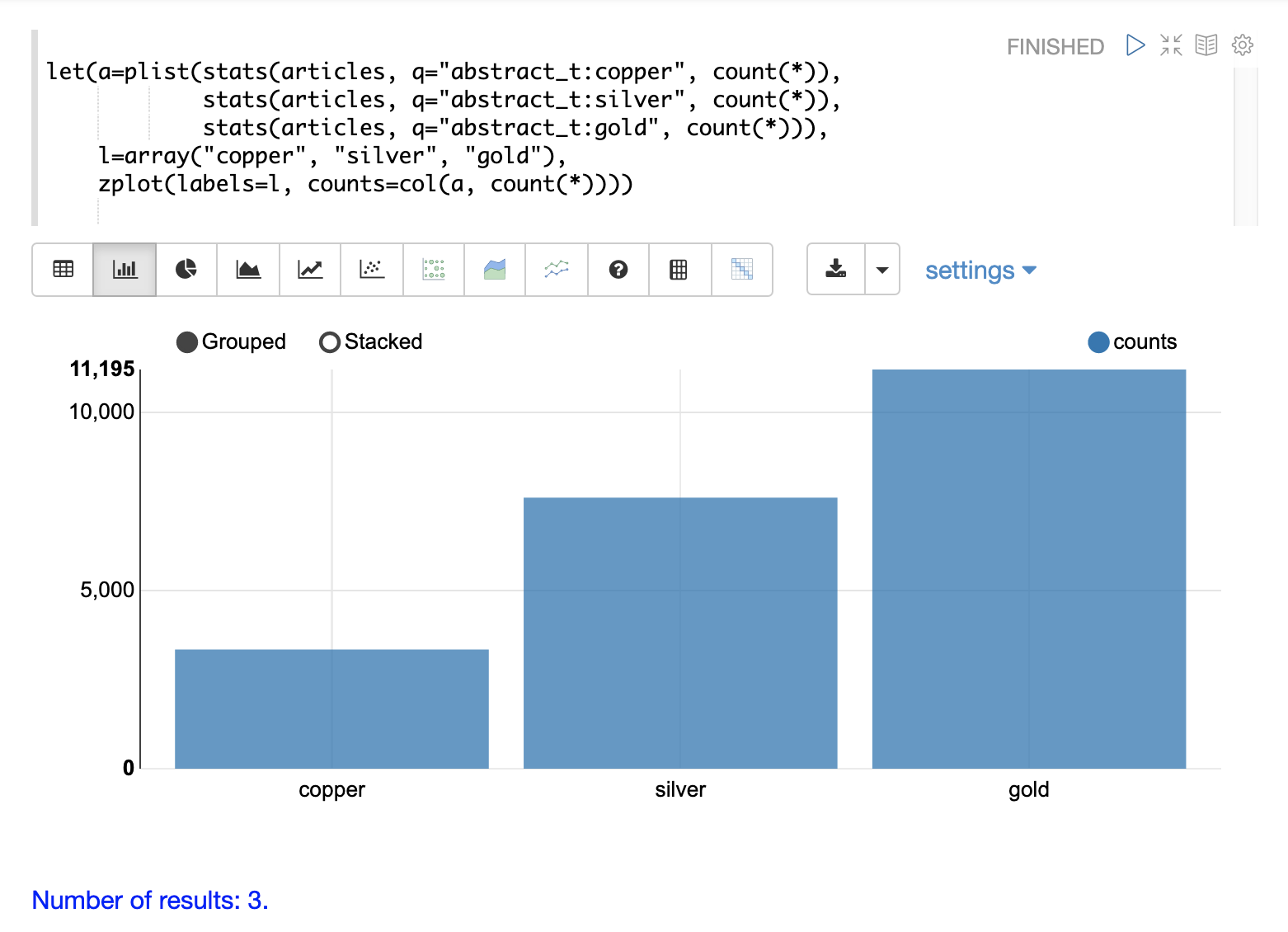
custom hist

頻率表

freqTable 函數會傳回離散資料集的頻率分佈。freqTable 函數不會像直方圖那樣建立組距。相反，它會計算每個離散資料值的出現次數，並傳回一個包含每個值的頻率統計資料的元組列表。

以下是根據股票代碼為 amzn 的每日開盤股價四捨五入的 差異 結果集建立的頻率表示例。

這個範例很有趣，因為它展示了達到結果的多步驟過程。第一步是在 stocks 集合中 搜尋 股票代碼為 amzn 的記錄。請注意，結果集依日期升序排序，並傳回 open_d 欄位，這是當天的開盤價。

然後將 open_d 欄位向量化並設定為變數 b，現在其中包含按日期升序排序的開盤價向量。

接著使用 diff 函數計算開盤價向量的 一階差分。一階差分只是從陣列中的每個值減去前一個值。這將提供每日價格差異的陣列，其中將顯示每日開盤價的變化。

然後使用 round 函數將價格差異四捨五入到最接近的整數，以建立離散值向量。此範例中的 round 函數有效地在整數邊界 分組 連續資料。

最後，在離散值上執行 freqTable 函數以計算頻率表。

let(a=search(stocks,
             q="ticker_s:amzn",
             fl="open_d, date_dt",
             sort="date_dt asc",
             rows=25000),
    b=col(a, open_d),
    c=diff(b),
    d=round(c),
    e=freqTable(d))

當此運算式傳送至 /stream 處理器時，它會回應

 {
   "result-set": {
     "docs": [
       {
         "pct": 0.00019409937888198756,
         "count": 1,
         "cumFreq": 1,
         "cumPct": 0.00019409937888198756,
         "value": -57
       },
       {
         "pct": 0.00019409937888198756,
         "count": 1,
         "cumFreq": 2,
         "cumPct": 0.00038819875776397513,
         "value": -51
       },
       {
         "pct": 0.00019409937888198756,
         "count": 1,
         "cumFreq": 3,
         "cumPct": 0.0005822981366459627,
         "value": -49
       },
       ...
       ]}}

使用 Zeppelin-Solr，頻率表可以首先視覺化為表格

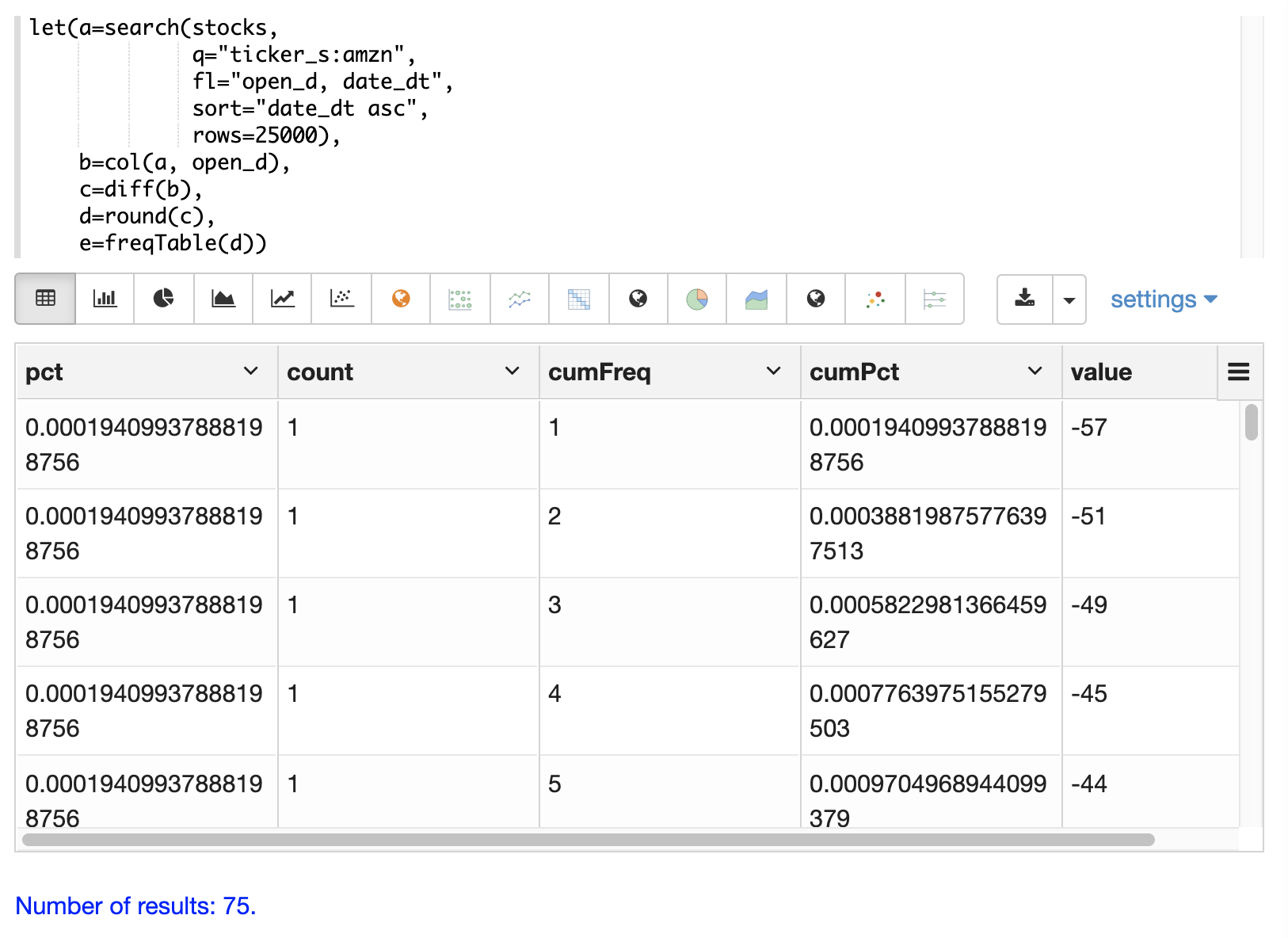
freqTable

然後，可以透過切換到散佈圖並為 x 軸選取 value 欄位，並為 y 軸選取 count 欄位來繪製頻率表

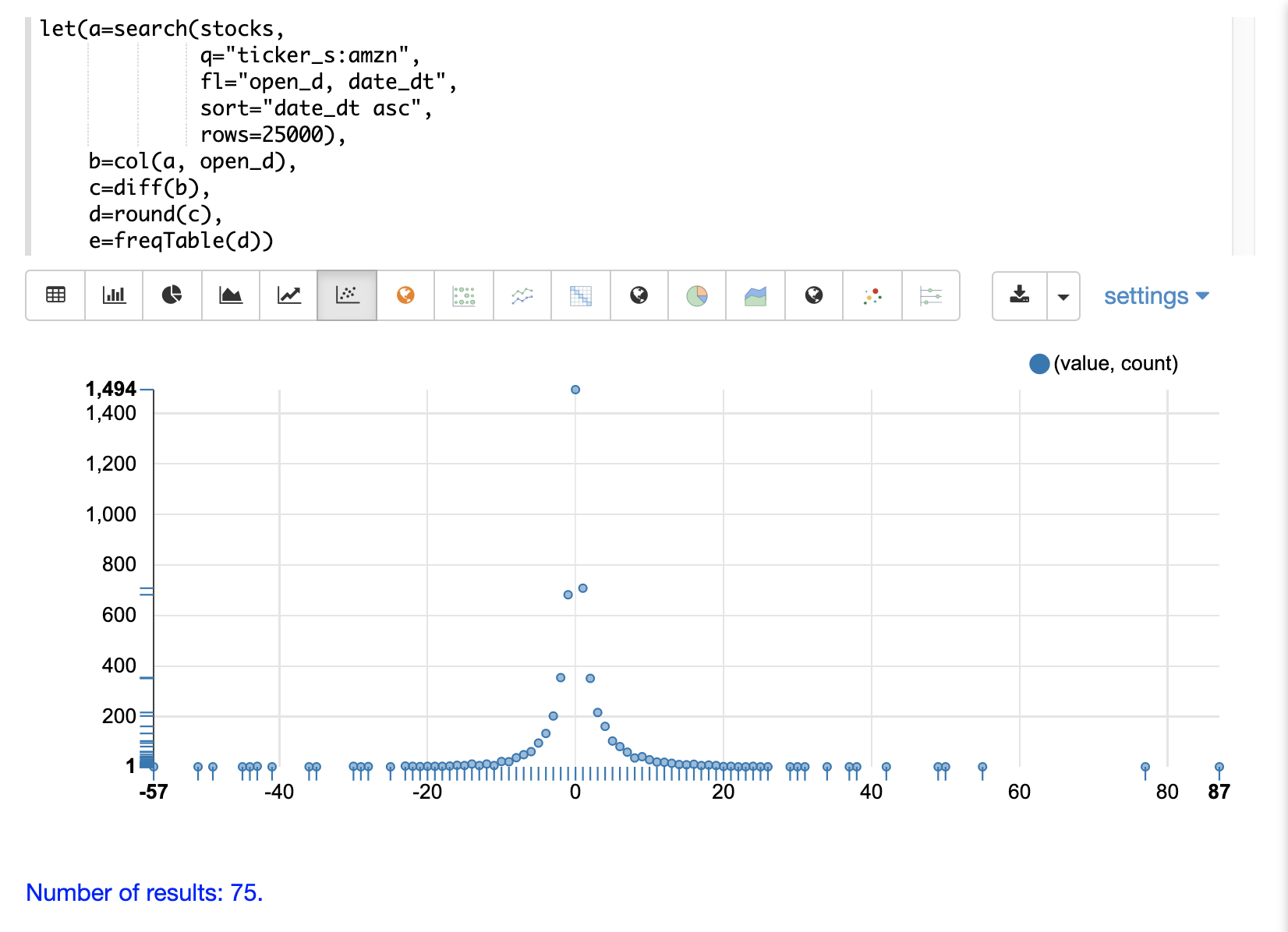
freqTable1

請注意，視覺化效果可以清楚地顯示四捨五入為整數的每日股價變化頻率。最常出現的值是 0，出現 1494 次，其次是 -1 和 1，出現約 700 次。

百分位數

percentile 函數會傳回樣本集中特定百分位數的估計值。下面的範例會傳回一個包含 logs 集合中 response_d 欄位的隨機樣本。response_d 欄位會被向量化，並計算向量的第 20 個百分位數

let(a=random(logs, q="*:*", rows="15000", fl="response_d"),
    b=col(a, response_d),
    c=percentile(b, 20))

當此運算式傳送至 /stream 處理器時，它會回應

 {
   "result-set": {
     "docs": [
       {
         "c": 818.073554
       },
       {
         "EOF": true,
         "RESPONSE_TIME": 286
       }
     ]
   }
 }

percentile 函數也可以計算百分位數值陣列。下面的範例計算 response_d 欄位隨機樣本的第 20、40、60 和 80 個百分位數

let(a=random(logs, q="*:*", rows="15000", fl="response_d"),
    b=col(a, response_d),
    c=percentile(b, array(20,40,60,80)))

當此運算式傳送至 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "c": [
          818.0835543394625,
          843.5590348165282,
          866.1789509894824,
          892.5033386599067
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 291
      }
    ]
  }
}

分位數圖

分位數圖或 QQ 圖是視覺比較兩個或多個分佈的強大工具。

分位數圖會在同一個視覺化效果中繪製兩個或多個分佈的百分位數。這允許在每個百分位數上視覺比較分佈。一個簡單的範例將有助於說明分位數圖的強大功能。

在此範例中，兩個股票代碼 goog 和 amzn 的每日股價變化分佈會使用分位數圖進行視覺化。

該範例首先建立一個代表將要計算的百分位數值的陣列，並將此陣列設定為變數 p。然後，從股票代碼 amzn 和 goog 中繪製 change_d 欄位的隨機樣本。change_d 欄位代表一天的股價變化。然後將 change_d 欄位向量化，並將兩個樣本分別放入變數 amzn 和 goog 中。然後使用 percentile 函數計算兩個向量的百分位數。請注意，變數 p 用於指定要計算的百分位數清單。

最後，使用 zplot 在 x 軸上繪製百分位數序列，並在 y 軸上繪製兩個分佈的計算百分位數值。並使用折線圖視覺化 QQ 圖。

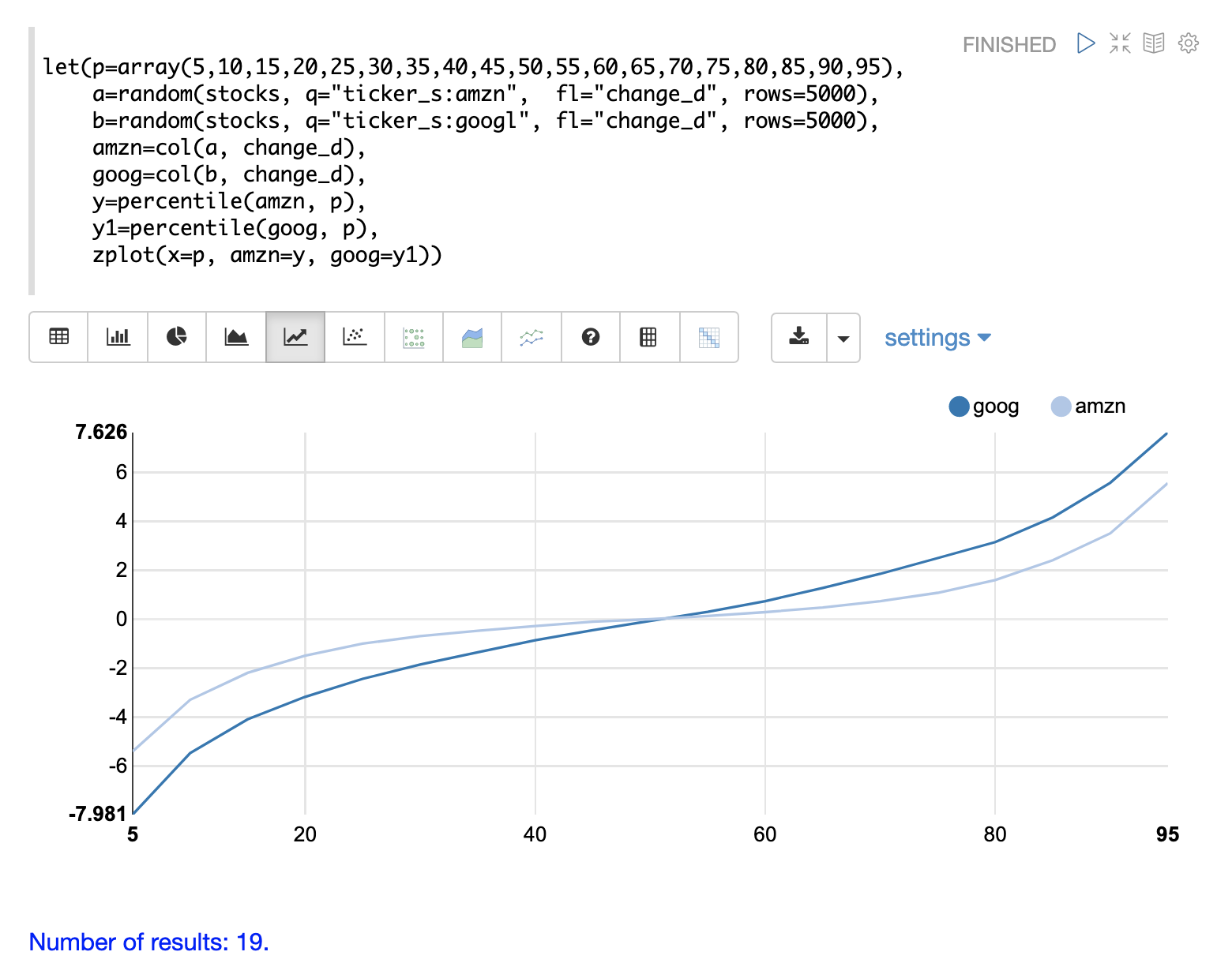
quantile plot

此分位數圖清楚地顯示了 amzn 和 googl 每日價格變化分佈。在圖表中，x 軸為百分位數，y 軸為計算的百分位數值。

請注意，goog 百分位數值開始時較低，結尾時高於 amzn 圖，並且斜率更陡峭。這顯示 goog 價格變化分佈的變異性更大。該圖清楚地顯示了跨越整個百分位數範圍的分佈差異。

相關性和共變異數

相關性和共變異數衡量隨機變數如何一起波動。

相關性和相關矩陣

相關性是衡量兩個向量之間線性相關性的指標。相關性的範圍介於 -1 和 1 之間。

支援三種相關性類型

  • pearsons (預設)

  • kendalls

  • spearmans

相關性類型是透過在函數呼叫中加入 type 具名參數來指定。

在下面的範例中，使用 random 函數從 logs 集合中繪製包含兩個欄位 filesize_d 和 response_d 的隨機樣本。這些欄位被向量化為變數 x 和 y，然後使用 corr 函數計算兩個向量的 Spearman’s 相關性。

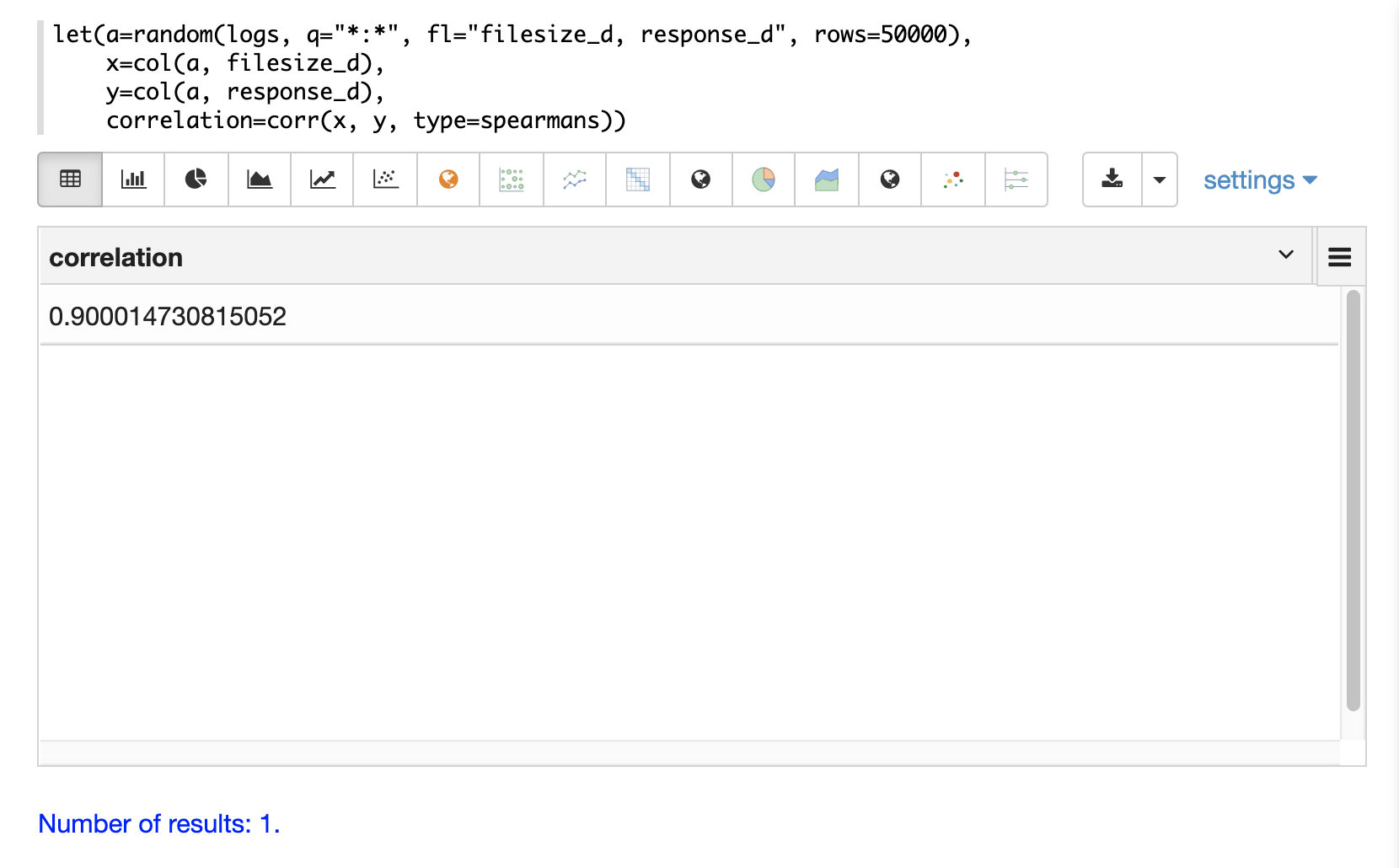
correlation

相關矩陣

相關矩陣是視覺化兩個或多個向量之間相關性的強大工具。

如果將矩陣作為參數傳遞，corr 函數會建立相關矩陣。相關矩陣是透過關聯矩陣的 欄來計算的。

下面的範例展示了相關矩陣與二維分面結合的強大功能。

在此範例中，facet2D 函數用於在 nyc311 投訴資料庫的 complaint_type_s 和 zip_s 欄位上產生二維分面彙總。彙總前 20 個投訴類型和每個投訴類型的前 25 個郵遞區號。結果是包含 complaint_type_s、zip_s 和該配對計數的元組資料流。

然後使用 pivot 函數將欄位透視為 矩陣，其中 zip_s 欄位為 列，complaint_type_s 欄位為 欄。count(*) 欄位會填入矩陣的儲存格中的值。

然後使用 corr 函數關聯矩陣的 欄。這會產生一個相關矩陣，顯示投訴類型如何根據它們出現的郵遞區號相關聯。另一種看待此問題的方式是，它顯示不同的投訴類型在各個郵遞區號中傾向於如何同時出現。

最後，使用 zplot 函數將相關矩陣繪製為熱圖。

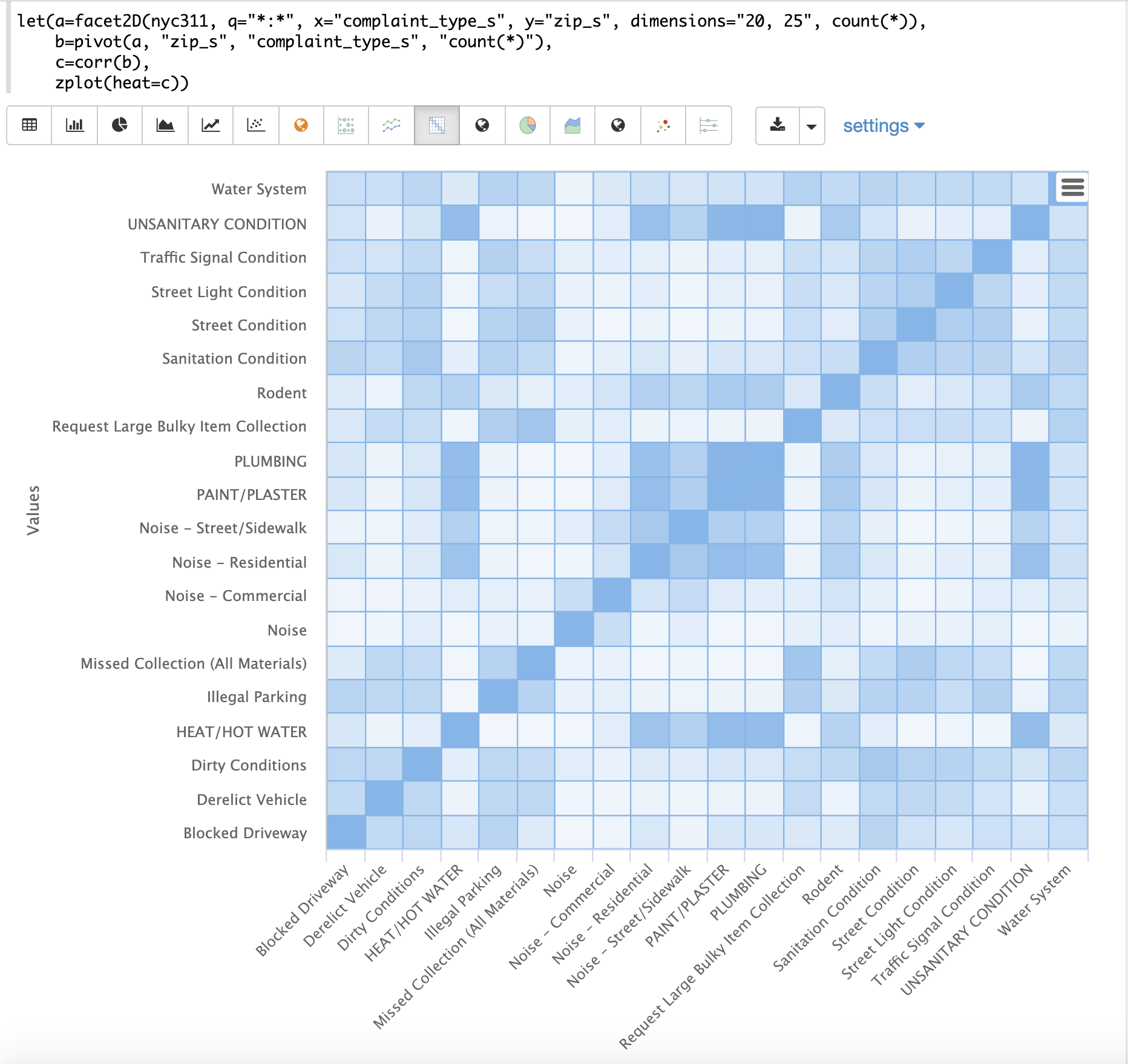
corrmatrix

請注意，在此範例中，相關矩陣是正方形的，在 x 和 y 軸上都顯示投訴類型。熱圖中儲存格的顏色顯示投訴類型之間相關性的強度。

熱圖是互動式的，因此將滑鼠游標移到其中一個儲存格上會彈出該儲存格的值。

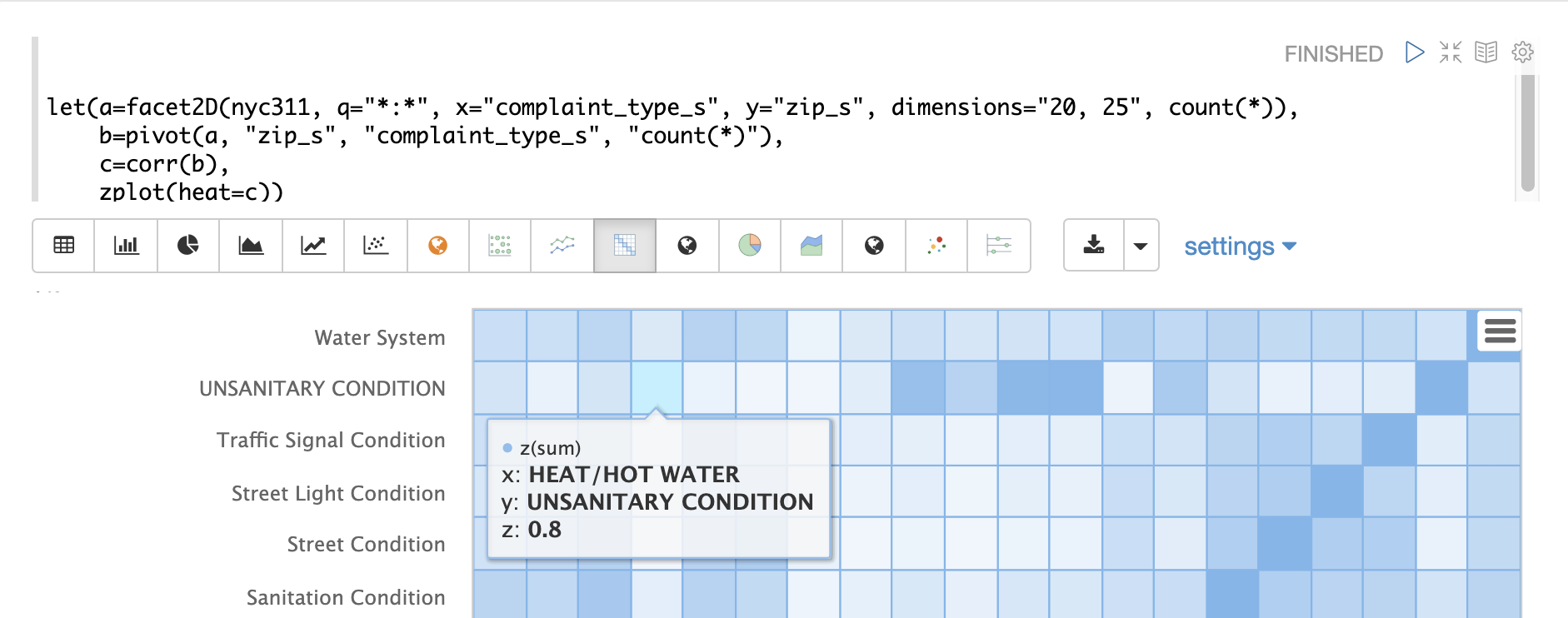
corrmatrix2

請注意，HEAT/HOT WATER 和 UNSANITARY CONDITION 投訴的相關性為 8 (四捨五入到最接近的十分之一)。

共變異數和共變異數矩陣

共變異數是未縮放的相關性度量。

cov 函數會計算兩個資料向量的共變異數。

在下面的範例中，使用 random 函數從 logs 集合中繪製包含兩個欄位 filesize_d 和 response_d 的隨機樣本。這些欄位被向量化為變數 x 和 y，然後使用 cov 函數計算兩個向量的共變異數。

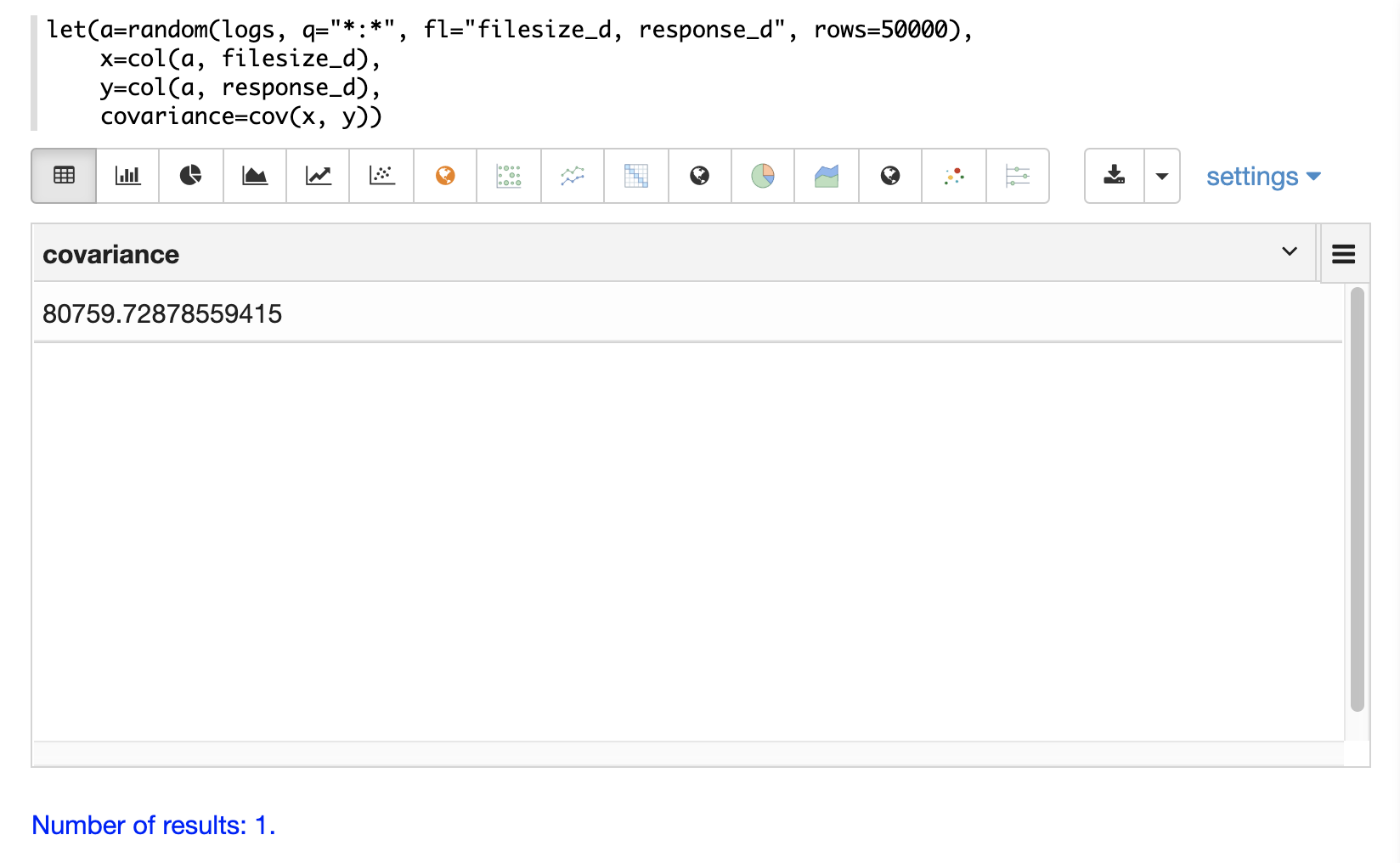
covariance

如果將矩陣傳遞給 cov 函數，它會自動計算矩陣 欄的共變異數矩陣。

請注意，在下面的範例中，x 和 y 向量會加入到一個矩陣中。然後，將矩陣轉置以將列轉換為欄，並計算矩陣欄的共變異數矩陣。

let(a=random(logs, q="*:*", fl="filesize_d, response_d", rows=50000),
    x=col(a, filesize_d),
    y=col(a, response_d),
    m=transpose(matrix(x, y)),
    covariance=cov(m))

當此運算式傳送至 /stream 處理器時，它會回應

 {
   "result-set": {
     "docs": [
       {
         "covariance": [
           [
             4018404.072532102,
             80243.3948172242
           ],
           [
             80243.3948172242,
             1948.3216661122592
           ]
         ]
       },
       {
         "EOF": true,
         "RESPONSE_TIME": 534
       }
     ]
   }
 }

共變異數矩陣包含兩個向量的變異數和向量之間的共變異數，格式如下

         x                 y
 x [4018404.072532102, 80243.3948172242],
 y [80243.3948172242,  1948.3216661122592]

共變異數矩陣永遠是正方形的。因此，從 3 個向量建立的共變異數矩陣會產生一個 3 x 3 的矩陣。

統計推論檢定

統計推論檢定會檢定 隨機樣本上的假設，並傳回可用於推斷整個族群檢定可靠性的 p 值。

提供下列統計推論檢定

  • anova：單向變異數分析檢定兩個或多個隨機樣本的平均值是否存在統計上的顯著差異。

  • ttest：T 檢定會檢定兩個隨機樣本的平均值是否存在統計上的顯著差異。

  • pairedTtest：配對 t 檢定會檢定具有配對資料的兩個隨機樣本的平均值是否存在統計上的顯著差異。

  • gTestDataSet：G 檢定會檢定是否從同一個族群中抽取了兩個分組離散資料的樣本。

  • chiSquareDataset：卡方檢定會檢定是否從同一個族群中抽取了兩個分組離散資料的樣本。

  • mannWhitney：曼-惠特尼檢定是一種非參數檢定，用於檢測兩個連續數據樣本是否來自同一個母體。當 T 檢定的基本假設不成立時，通常會使用曼-惠特尼檢定來替代 T 檢定。

  • ks：科摩哥洛夫-史密諾夫檢定用於檢測兩個連續數據樣本是否來自同一個分佈。

下方是一個對兩個隨機樣本執行 T 檢定的簡單範例。返回的 p 值為 0.93，表示我們可以接受虛無假設，即這兩個樣本在均值方面沒有統計上的顯著差異。

let(a=random(collection1, q="*:*", rows="1500", fl="price_f"),
    b=random(collection1, q="*:*", rows="1500", fl="price_f"),
    c=col(a, price_f),
    d=col(b, price_f),
    e=ttest(c, d))

當此運算式傳送至 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "e": {
          "p-value": 0.9350135639249795,
          "t-statistic": 0.081545541074817
        }
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 48
      }
    ]
  }
}

轉換

在統計分析中，通常在執行統計計算之前轉換數據集會很有用。統計函數庫包含以下常用的轉換：

  • rank：返回一個數值陣列，其中包含原始陣列中每個元素的等級轉換值。

  • log：返回一個數值陣列，其中包含原始陣列中每個元素的自然對數。

  • log10：返回一個數值陣列，其中包含原始陣列中每個元素的以 10 為底的對數。

  • sqrt：返回一個數值陣列，其中包含原始陣列中每個元素的平方根。

  • cbrt：返回一個數值陣列，其中包含原始陣列中每個元素的立方根。

  • recip：返回一個數值陣列，其中包含原始陣列中每個元素的倒數。

下方是一個對數轉換數據集執行 t 檢定的範例

let(a=random(collection1, q="*:*", rows="1500", fl="price_f"),
    b=random(collection1, q="*:*", rows="1500", fl="price_f"),
    c=log(col(a, price_f)),
    d=log(col(b, price_f)),
    e=ttest(c, d))

當此運算式傳送至 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "e": {
          "p-value": 0.9655110070265056,
          "t-statistic": -0.04324265449471238
        }
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 58
      }
    ]
  }
}

反轉換

已使用 log、log10、sqrt 和 cbrt 函數轉換的向量可以使用 pow 函數進行反轉換。

下面的範例顯示如何反轉換已使用 sqrt 函數轉換的數據。

let(echo="b,c",
    a=array(100, 200, 300),
    b=sqrt(a),
    c=pow(b, 2))

當此運算式傳送至 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "b": [
          10,
          14.142135623730951,
          17.320508075688775
        ],
        "c": [
          100,
          200.00000000000003,
          300.00000000000006
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

下面的範例顯示如何反轉換已使用 log10 函數轉換的數據。

let(echo="b,c",
    a=array(100, 200, 300),
    b=log10(a),
    c=pow(10, b))

當此運算式傳送至 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "b": [
          2,
          2.3010299956639813,
          2.4771212547196626
        ],
        "c": [
          100,
          200.00000000000003,
          300.0000000000001
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

已使用 recip 函數轉換的向量可以透過取倒數的倒數來進行反轉換。

下面的範例顯示了 recip 函數的反轉換範例。

let(echo="b,c",
    a=array(100, 200, 300),
    b=recip(a),
    c=recip(b))

當此運算式傳送至 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "b": [
          0.01,
          0.005,
          0.0033333333333333335
        ],
        "c": [
          100,
          200,
          300
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

Z 分數

zscores 函數將數值陣列轉換為 Z 分數陣列。 Z 分數表示一個數字與平均值的標準差個數。

下面的範例計算陣列中值的 Z 分數。

let(a=array(1,2,3),
    b=zscores(a))

當此運算式傳送至 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "b": [
          -1,
          0,
          1
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 27
      }
    ]
  }
}