線性迴歸

數學運算式庫支援簡單和多元線性迴歸。

簡單線性迴歸

regress 函式用於在兩個隨機變數之間建立線性迴歸模型。樣本觀察值使用兩個數值陣列提供。第一個數值陣列是自變數，第二個陣列是應變數。

在下面的範例中，random 函式選取 50000 個隨機樣本，每個樣本都包含 filesize_d 和 response_d 欄位。這兩個欄位會向量化並儲存在變數 x 和 y 中。然後，regress 函式對這兩個數值陣列執行迴歸分析。

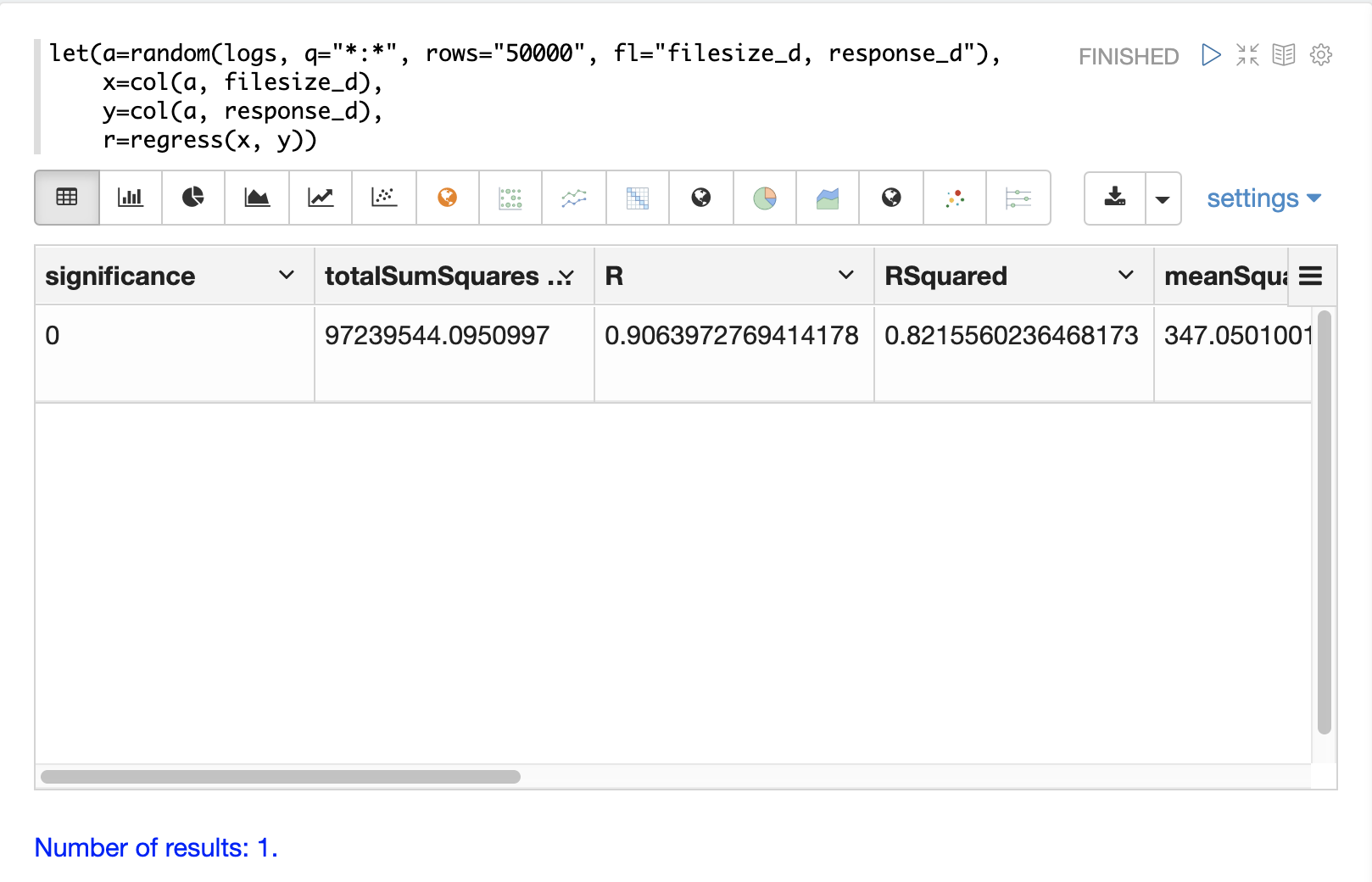
regress 函式會傳回包含迴歸分析結果的單一元組。

let(a=random(logs, q="*:*", rows="50000", fl="filesize_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, response_d),
    r=regress(x, y))

請注意，在此迴歸分析中，RSquared 的值為 .75。這表示 filesize_d 的變更解釋了 response_d 變數 75% 的變異性

{
  "result-set": {
    "docs": [
      {
        "significance": 0,
        "totalSumSquares": 96595678.64838874,
        "R": 0.9052835767815126,
        "RSquared": 0.8195383543903288,
        "meanSquareError": 348.6502485633668,
        "intercept": 55.64040842391729,
        "slopeConfidenceInterval": 0.0000822026526346821,
        "regressionSumSquares": 79163863.52071753,
        "slope": 0.019984612363694493,
        "interceptStdErr": 1.6792610845256566,
        "N": 50000
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 344
      }
    ]
  }
}

診斷結果可以使用 Zeppelin-Solr 在表格中視覺化。

diagnostics

預測

predict 函式使用迴歸模型進行預測。使用上述範例，迴歸模型可用於在給定 filesize_d 的值的情況下預測 response_d 的值。

在下面的範例中，predict 函式使用迴歸分析來預測 filesize_d 值為 40000 時 response_d 的值。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, response_d),
    r=regress(x, y),
    p=predict(r, 40000))

當此運算式傳送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "p": 748.079241022975
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 95
      }
    ]
  }
}

predict 函式也可以針對一組值進行預測。在這種情況下，它會傳回一組預測值。

在下面的範例中，predict 函式使用迴歸分析來預測用於產生模型的 5000 個 filesize_d 樣本中的每一個的值。在這種情況下，會傳回 5000 個預測值。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, response_d),
    r=regress(x, y),
    p=predict(r, x))

當此運算式傳送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "p": [
          742.2525322514165,
          709.6972488729955,
          687.8382568904871,
          820.2511324266264,
          720.4006432289061,
          761.1578181053039,
          759.1304101159126,
          699.5597256337142,
          742.4738911248204,
          769.0342605881644,
          746.6740473150268
          ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 113
      }
    ]
  }
}

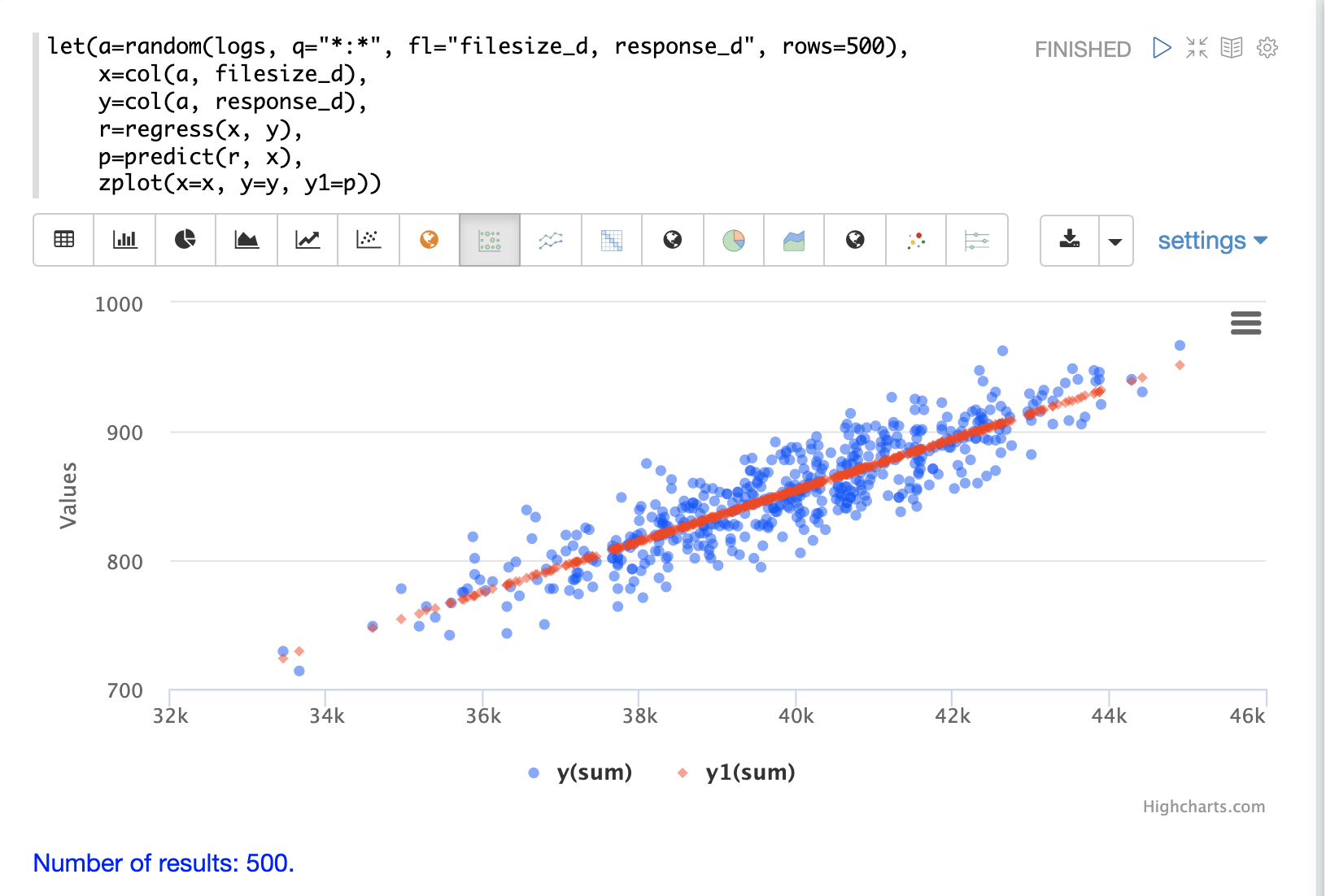
迴歸圖

使用 zplot 和 Zeppelin-Solr 直譯器，我們可以在同一個散佈圖中視覺化觀察值和預測值。在下面的範例中，zplot 將 filesize_d 觀察值繪製在 x 軸上，response_d 觀察值繪製在 y 軸上，而預測值則繪製在 y1 軸上。

linear

殘差

觀察值和預測值之間的差異稱為殘差。雖然沒有特定的函數來計算殘差，但可以使用向量數學來執行計算。

在下面的範例中，預測值儲存在變數 p 中。接著使用 ebeSubtract 函數從儲存在變數 y 中的實際 response_d 值中減去預測值。變數 e 包含殘差的陣列。

let(a=random(logs, q="*:*", rows="500", fl="filesize_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, response_d),
    r=regress(x, y),
    p=predict(r, x),
    e=ebeSubtract(y, p))

當此運算式傳送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "e": [
          31.30678554491226,
          -30.292830927953446,
          -30.49508862647258,
          -30.499884780783532,
          -9.696458959319784,
          -30.521563961535094,
          -30.28380938033081,
          -9.890289849359306,
          30.819723560583157,
          -30.213178859683012,
          -30.609943619066826,
          10.527700442607625,
          10.68046928406568
          ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 113
      }
    ]
  }
}

殘差圖

使用 zplot 和 Zeppelin-Solr，我們可以透過殘差圖來視覺化殘差。下面的殘差圖範例將預測值繪製在 x 軸上，將預測的誤差繪製在 y 軸上。

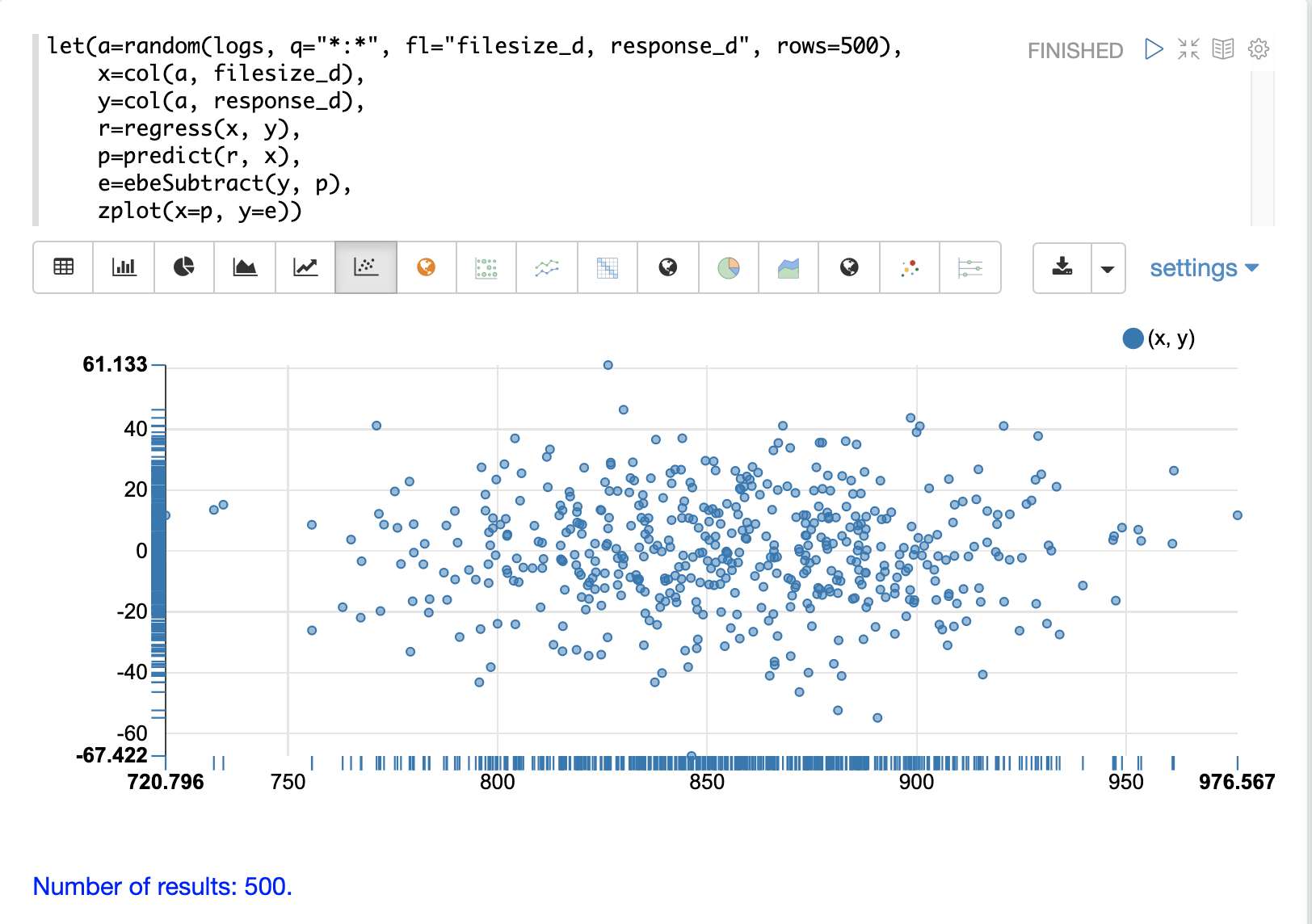
residual plot

殘差圖可用於解釋模型的可靠性。需要注意三件事：

  1. 殘差的分佈看起來是否為平均值為 0 的常態分佈？這讓解釋模型的結果更容易，以確定誤差的分佈對於預測是否可接受。這也讓在新預測中將殘差模型用於異常檢測更容易。

  2. 殘差看起來是否為異質變異？這表示殘差的變異數在整個預測範圍內是否相同？透過將預測繪製在 x 軸上，將誤差繪製在 y 軸上，我們可以查看變異性是否隨著預測值的增加而保持不變。如果殘差是異質變異的，則表示我們可以信任模型的誤差在整個預測範圍內是一致的。

  3. 殘差是否有任何模式？如果有的話，則表示資料中可能仍有需要建模的訊號。

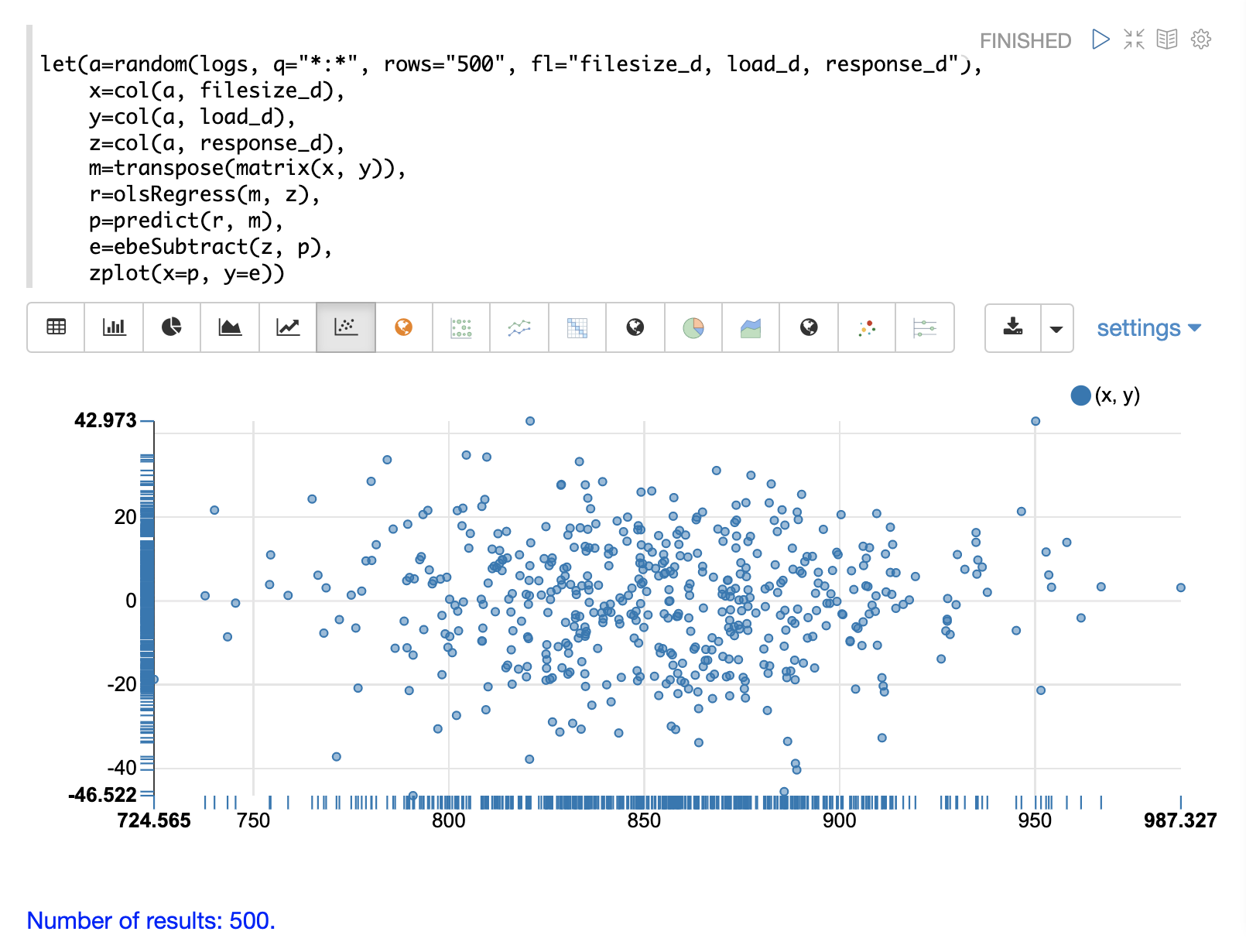
多元線性迴歸

olsRegress 函數執行多元線性迴歸分析。多元線性迴歸對兩個或多個自變數和一個應變數之間的線性關係進行建模。

下面的範例透過引入一個名為 load_d 的新自變數來擴展簡單線性迴歸範例。load_d 變數是下載檔案時網路上的負載。

請注意，兩個自變數 filesize_d 和 load_d 被向量化並儲存在變數 b 和 c 中。然後將變數 b 和 c 作為列添加到 matrix 中。然後將矩陣轉置，以便矩陣中的每一列代表一個具有 filesize_d 和 service_d 的觀察值。然後，olsRegress 函數使用觀察值矩陣作為自變數，並使用儲存在變數 d 中的 response_d 值作為應變數，執行多元迴歸分析。

let(a=random(testapp, q="*:*", rows="30000", fl="filesize_d, load_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, load_d),
    z=col(a, response_d),
    m=transpose(matrix(x, y)),
    r=olsRegress(m, z))

請注意，回應中迴歸分析的 RSquared 為 1。這表示 filesize_d 和 service_d 之間的線性關係描述了 response_d 變數 100% 的變異性。

{
  "result-set": {
    "docs": [
      {
        "regressionParametersStandardErrors": [
          1.7792032752524236,
          0.0000429945089590394,
          0.0008592489428291642
        ],
        "RSquared": 0.8850359458670845,
        "regressionParameters": [
          0.7318766882597804,
          0.01998298784650873,
          0.10982104952105468
        ],
        "regressandVariance": 1938.8190758686717,
        "regressionParametersVariance": [
          [
            0.014201127587649602,
            -3.326633951803927e-7,
            -0.000001732754417954437
          ],
          [
            -3.326633951803927e-7,
            8.292732891338694e-12,
            2.0407522508189773e-12
          ],
          [
            -0.000001732754417954437,
            2.0407522508189773e-12,
            3.3121477630934995e-9
          ]
        ],
        "adjustedRSquared": 0.8850282808303053,
        "residualSumSquares": 6686612.141261716
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 374
      }
    ]
  }
}

預測

predict 函數也可用於對多元線性迴歸進行預測。

下面是一個使用多元線性迴歸模型和單一觀察值進行單一預測的範例。觀察值是一個陣列，其結構與用於建立模型的觀察值矩陣相符。在此範例中，第一個值表示 filesize_d 為 40000，第二個值表示 load_d 為 4。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, load_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, load_d),
    z=col(a, response_d),
    m=transpose(matrix(x, y)),
    r=olsRegress(m, z),
    p=predict(r, array(40000, 4)))

當此運算式傳送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "p": 801.7725344814675
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 70
      }
    ]
  }
}

predict 函數也可以對多個多元觀察值進行預測。在這種情況下，會使用觀察值矩陣。

在下面的範例中，用於建立多元迴歸模型的觀察值矩陣被傳遞到 predict 函數，它會傳回一個預測陣列。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, load_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, load_d),
    z=col(a, response_d),
    m=transpose(matrix(x, y)),
    r=olsRegress(m, z),
    p=predict(r, m))

當此運算式傳送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "p": [
          917.7122088913725,
          900.5418518783401,
          871.7805676516689,
          822.1887964840801,
          828.0842807117554,
          785.1262470470162,
          833.2583851225845,
          802.016811579941,
          841.5253327135974,
          896.9648275225625,
          858.6511235977382,
          869.8381475112501
          ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 113
      }
    ]
  }
}

殘差

一旦產生預測值，可以使用與簡單線性迴歸相同的方法計算殘差。

下面是一個在多元線性迴歸之後計算殘差的範例。在此範例中，儲存在變數 g 中的預測值會從儲存在變數 d 中的觀察值中減去。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, load_d, response_d"),
    x=col(a, filesize_d),
    y=col(a, load_d),
    z=col(a, response_d),
    m=transpose(matrix(x, y)),
    r=olsRegress(m, z),
    p=predict(r, m),
    e=ebeSubtract(z, p))

當此運算式傳送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "e": [
          21.452271655340496,
          9.647947283595727,
          -23.02328008866334,
          -13.533046479596806,
          -16.1531952414299,
          4.966514036315402,
          23.70151322413119,
          -4.276176642246014,
          10.781062392156628,
          0.00039750380267378205,
          -1.8307638852961645
          ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 113
      }
    ]
  }
}

殘差圖

多元線性迴歸的殘差圖與簡單線性迴歸的殘差圖相同。預測值繪製在 x 軸上，誤差繪製在 y 軸上。

residual plot2

多元線性迴歸的殘差圖可以使用與簡單線性迴歸完全相同的方式來解釋。