計算幾何

數學運算式使用者指南的本節介紹計算幾何函數。

凸包

凸包是封閉資料集的最小凸點集。數學運算式支援計算 2D 資料集的凸包。計算出凸包後，可以應用一組數學運算式函數來幾何描述和視覺化凸包。

視覺化

convexHull 函數可用於視覺化一組 2D 點周圍的邊界。邊界視覺化對於了解資料點相對於邊界的位置很有用。

在以下範例中，convexHull 函數用於視覺化 NYC311 投訴資料庫中老鼠目擊事件的一組緯度和經度點的邊界。可以對老鼠目擊事件周圍的邊界進行調查，以更好地了解老鼠可能如何進入或離開特定區域。

散佈圖

在視覺化凸包之前，通常有必要將 2D 點視覺化為散佈圖。

在此範例中，random 函數從 NYC311（投訴資料庫）集合中抽取符合「老鼠目擊事件」的投訴描述和郵遞區號為 11238 的記錄樣本。然後將緯度和經度欄位向量化，並將經度繪製在 x 軸上，緯度繪製在 y 軸上，以繪製散佈圖。

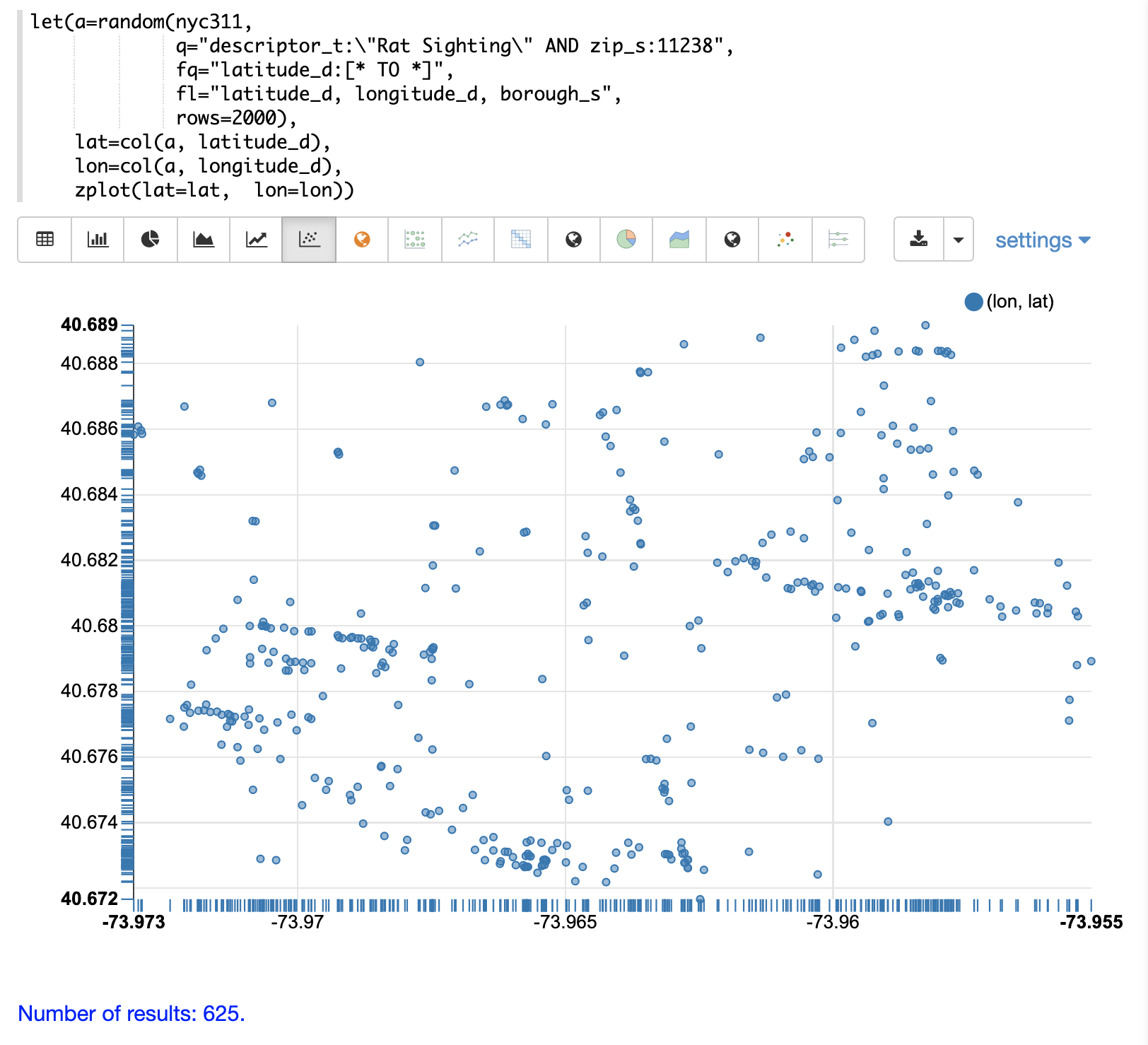
$convex0$

從散佈圖中注意到，許多點似乎位於圖的邊界附近。

凸包圖

convexHull 函數可用於視覺化邊界。此範例使用從 NYC311 資料庫中提取的相同點。但是，不是直接繪製點，而是將緯度和經度點作為列添加到矩陣中。然後使用 transpose 函數轉置矩陣，以便矩陣的每一列都包含一個緯度和經度點。

然後使用 convexHull 函數計算點矩陣的凸包。凸包設定為名為 hull 的變數。

一旦建立凸包後，可以使用 getVertices 函數來檢索散佈圖中組成散佈圖周圍凸邊界的點矩陣。然後可以使用 colAt 函數從矩陣中檢索緯度和經度向量，以便可以使用 zplot 函數將它們視覺化。在下面的示例中，凸包點被視覺化為散佈圖。

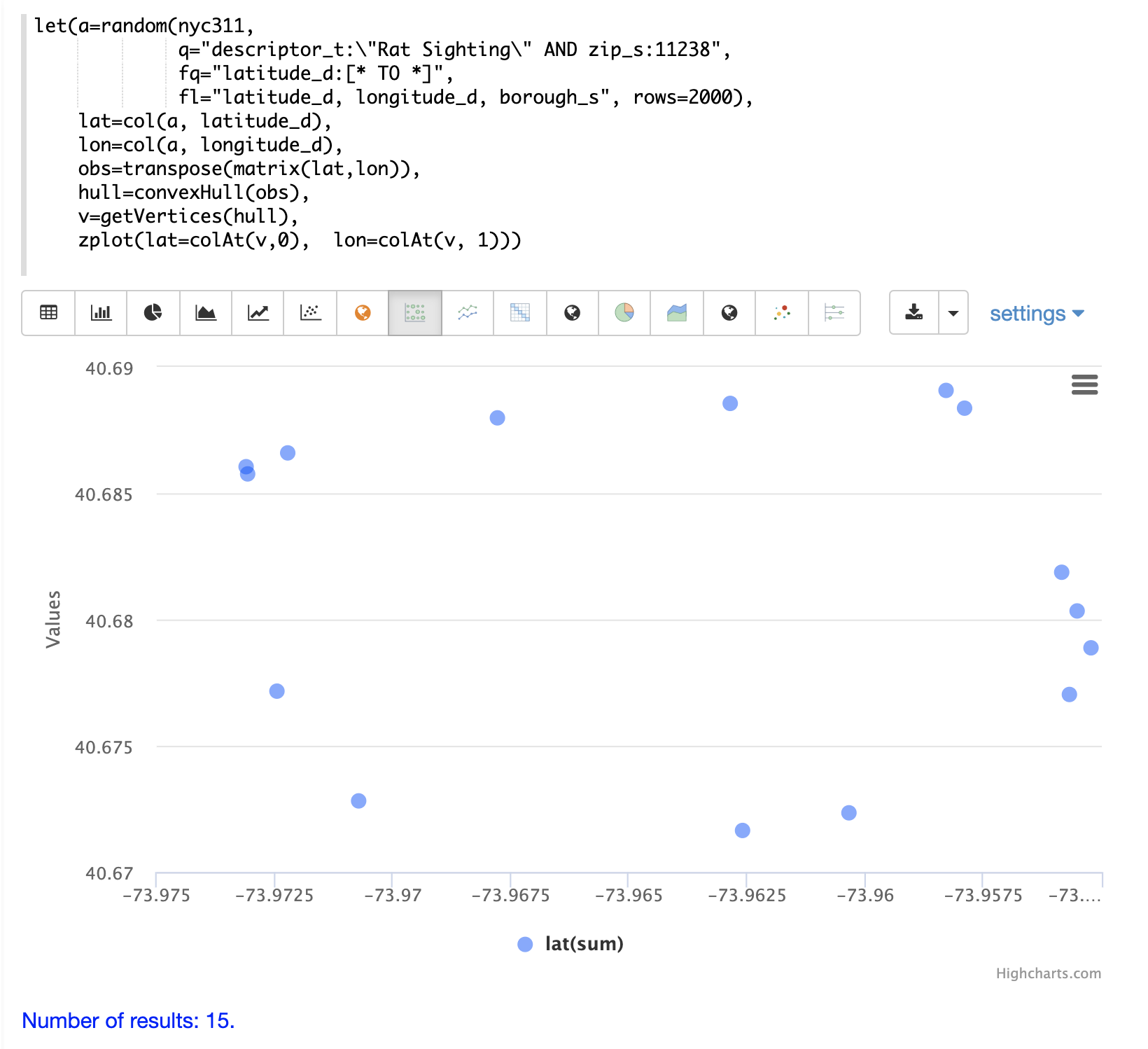
$hullplot$

請注意，散佈圖中的 15 個點描述了凸包的緯度和經度點。

投影和聚類

計算出凸包後，可以使用 projectToBorder 將點投影到邊界上最近的點。在下面的示例中，projectToBorder 函數用於將原始散佈圖點投影到最近的邊界。

projectToBorder 函數返回邊界投影的緯度/經度點矩陣。在示例中，然後使用 K-means 聚類將邊界點的矩陣聚類成 7 個群集。然後使用 zplot 函數繪製群集的邊界點。

$convex1$

在視覺化中，很容易看到邊界上哪些點的密度最高。在老鼠目擊事件的情況下，此資訊有助於了解老鼠最有可能從哪些邊界點進入或離開。

繪製質心

邊界點被聚類後，很容易從群集中提取質心並將它們繪製在地圖上。下面的示例使用 getCentroids 函數從群集中提取質心。getCentroids 返回代表邊界群集質心的緯度/經度點矩陣。然後可以使用 colAt 函數提取緯度/經度向量，以便可以使用 zplot 將它們繪製在地圖上。

$convex2$

上面的地圖顯示了邊界群集的質心。現在可以縮放和調查來自最高密度群集的質心，以確定哪些可能是開始邊界調查的最佳地點。

包圍圓盤

enclosingDisk 函數查找包圍 2D 資料集的最小包圍圓。一旦計算出包圍圓盤，就可以應用一組數學表達式函數來幾何地描述包圍圓盤。

在下面的示例中，為一組隨機生成的 1000 個 2D 觀測值計算包圍圓盤。

然後，在包圍圓盤上調用以下函數

getCenter：返回作為圓盤中心的 2D 點。
getRadius：返回圓盤的半徑。
getSupportPoints：返回圓盤的支援點。

let(echo="center, radius, support",
    x=sample(normalDistribution(0, 20), 1000),
    y=sample(normalDistribution(0, 20), 1000),
    observations=transpose(matrix(x,y)),
    disk=enclosingDisk(observations),
    center=getCenter(disk),
    radius=getRadius(disk),
    support=getSupportPoints(disk))

當此表達式發送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "center": [
          -6.668825009733749,
          -2.9825450908240025
        ],
        "radius": 72.66109546907208,
        "support": [
          [
            20.350992271739464,
            64.46791279377014
          ],
          [
            33.02079953093981,
            57.880978456420365
          ],
          [
            -44.7273247899923,
            -64.87911518353323
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 8
      }
    ]
  }
}