曲線擬合

polyfit 函式是一個通用曲線擬合器，用於模擬兩個隨機變數之間的非線性關係。

polyfit 函式會傳遞 x 軸和 y 軸，並將平滑曲線擬合到資料。如果只提供單一陣列，則會將其視為 y 軸，並為 x 軸產生序列。可以新增第三個參數來指定多項式的次數。如果未提供次數，則預設會使用 3 次多項式。次數越高，可以建模的曲線就越多。

polyfit 函式可以使用與 Zeppelin-Solr 線性迴歸類似的方式進行視覺化。

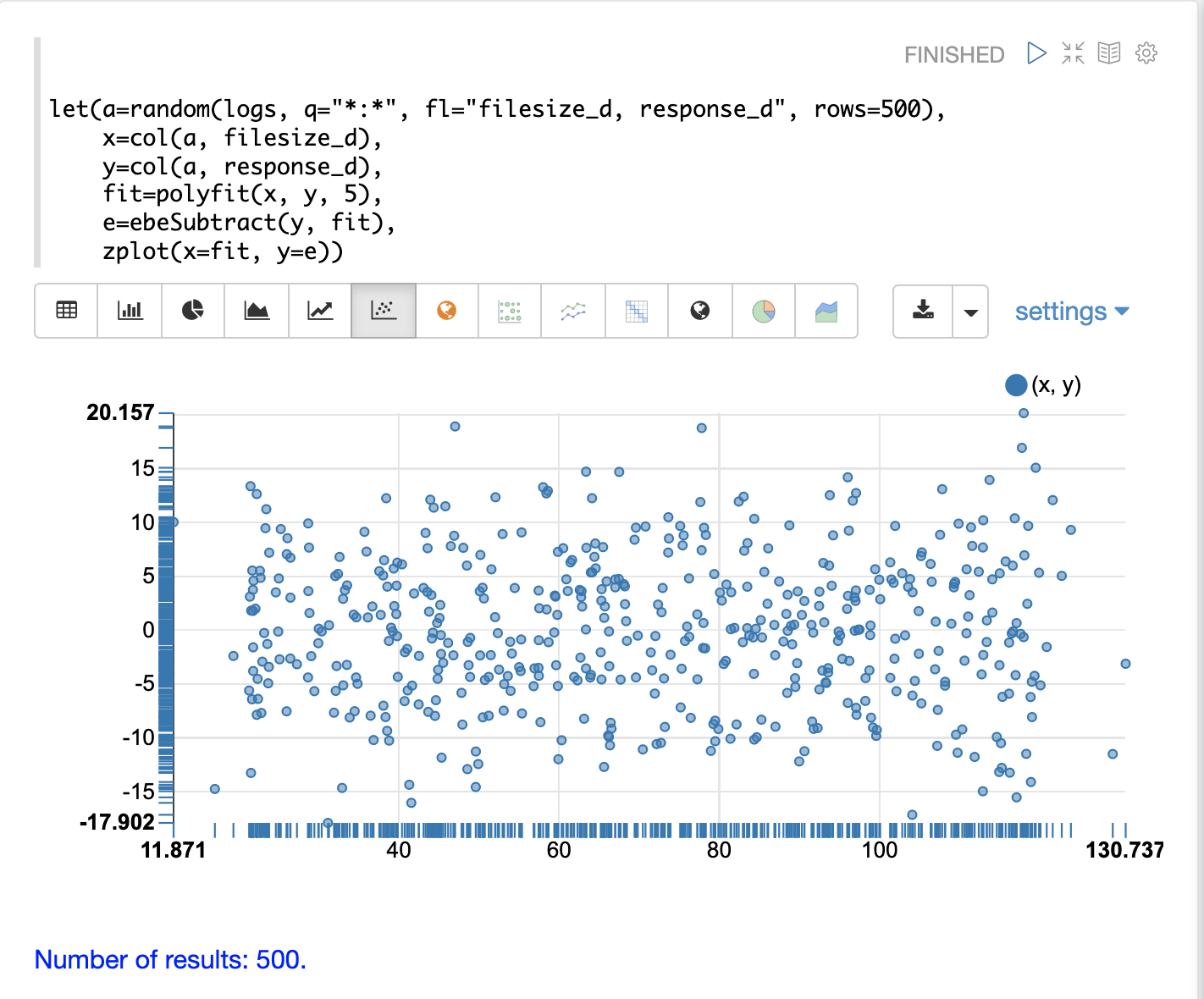
以下範例使用 polyfit 函式將非線性曲線擬合到隨機樣本的散佈圖。藍點是原始觀察值的散佈圖，紅點是預測的曲線。

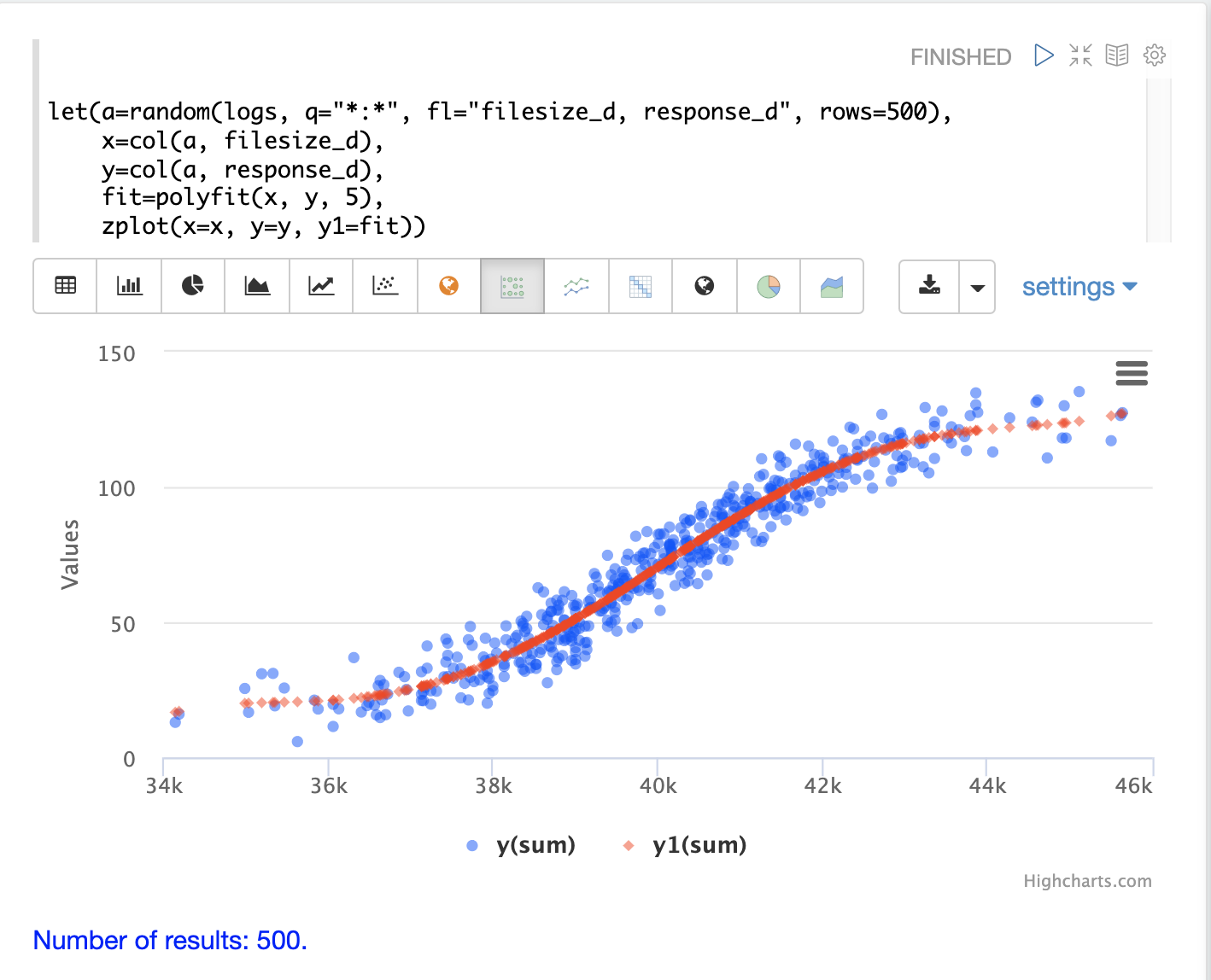
在上面的範例中，從 logs 集合中提取包含兩個欄位 filesize_d 和 response_d 的隨機樣本。這兩個欄位被向量化並設定為變數 x 和 y。

然後，polyfit 函式用於使用 5 次多項式將非線性模型擬合到資料。polyfit 函式傳回一個模型，然後該模型會與原始觀察值一起由 zplot 直接繪製。

擬合的模型也可以像線性迴歸一樣被 predict 函式使用。以下範例使用擬合模型來預測檔案大小為 42000 的回應時間。

如果提供了預測值陣列，則會傳回預測陣列。

polyfit 模型執行內插和外推，這表示它可以預測資料集範圍內和範圍外的結果。

gaussfit 函式會將平滑曲線擬合到高斯峰值。gaussfit 函式會採用 x 軸和 y 軸，並將平滑高斯曲線擬合到資料。如果僅傳遞一個數字向量，gaussfit 會將其視為 y 軸，並為 x 軸產生序列。

gaussfit 的有趣使用案例之一是視覺化迴歸模型的殘差與常態分佈的擬合程度。

一個良好擬合的回歸模型的特性之一是其殘差理想情況下會符合常態分佈。我們可以透過建立殘差的直方圖，然後將高斯曲線擬合到直方圖的曲線來測試這一點。

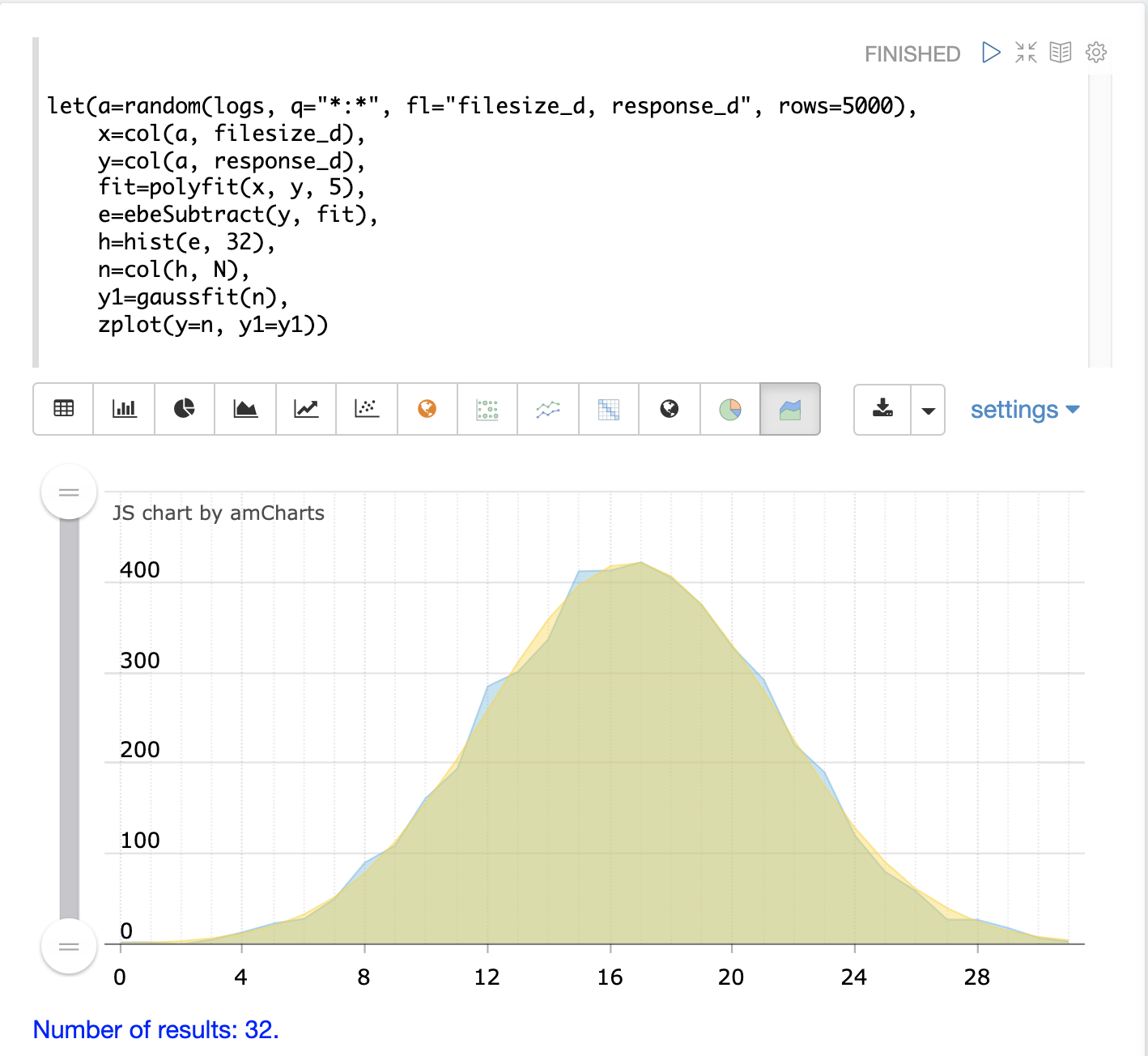
在下面的範例中，來自 polyfit 回歸的殘差使用 hist 函數建模，以返回具有 32 個箱子的直方圖。hist 函數會返回一個元組列表，其中包含每個箱子的統計資訊。在此範例中，col 函數用於返回一個向量，其中包含每個箱子的 N 列，也就是箱子中觀察值的計數。如果殘差呈常態分佈，我們會預期箱子的計數大致遵循高斯曲線。

接著，箱子計數向量會作為 y 軸傳遞給 gaussfit。gaussfit 會為 x 軸產生一個序列，然後將高斯曲線擬合到資料。

然後使用 zplot 來繪製原始箱子計數和擬合的曲線。在下面的範例中，藍色線是箱子計數，而平滑的黃色線是擬合的曲線。我們可以發現，分組的殘差與常態分佈相當符合。

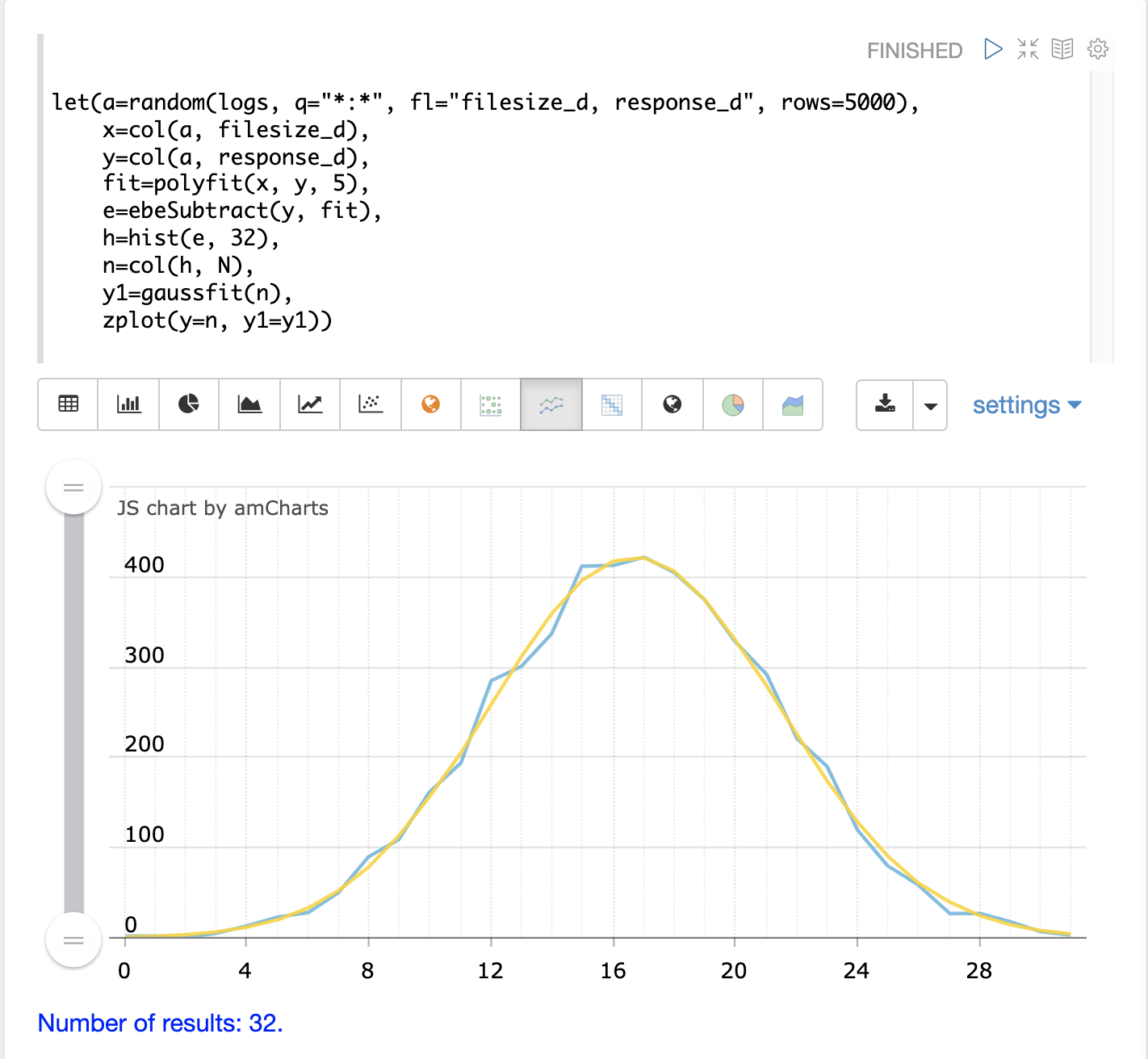
第二個圖表顯示了兩個曲線以面積圖重疊顯示。

harmonicFit 函數（或簡稱 harmfit）將一條平滑線擬合到正弦波的控制點。harmfit 函數會傳遞 x 軸和 y 軸，並將平滑曲線擬合到資料。如果提供單一陣列，則將其視為 y 軸，並為 x 軸產生一個序列。

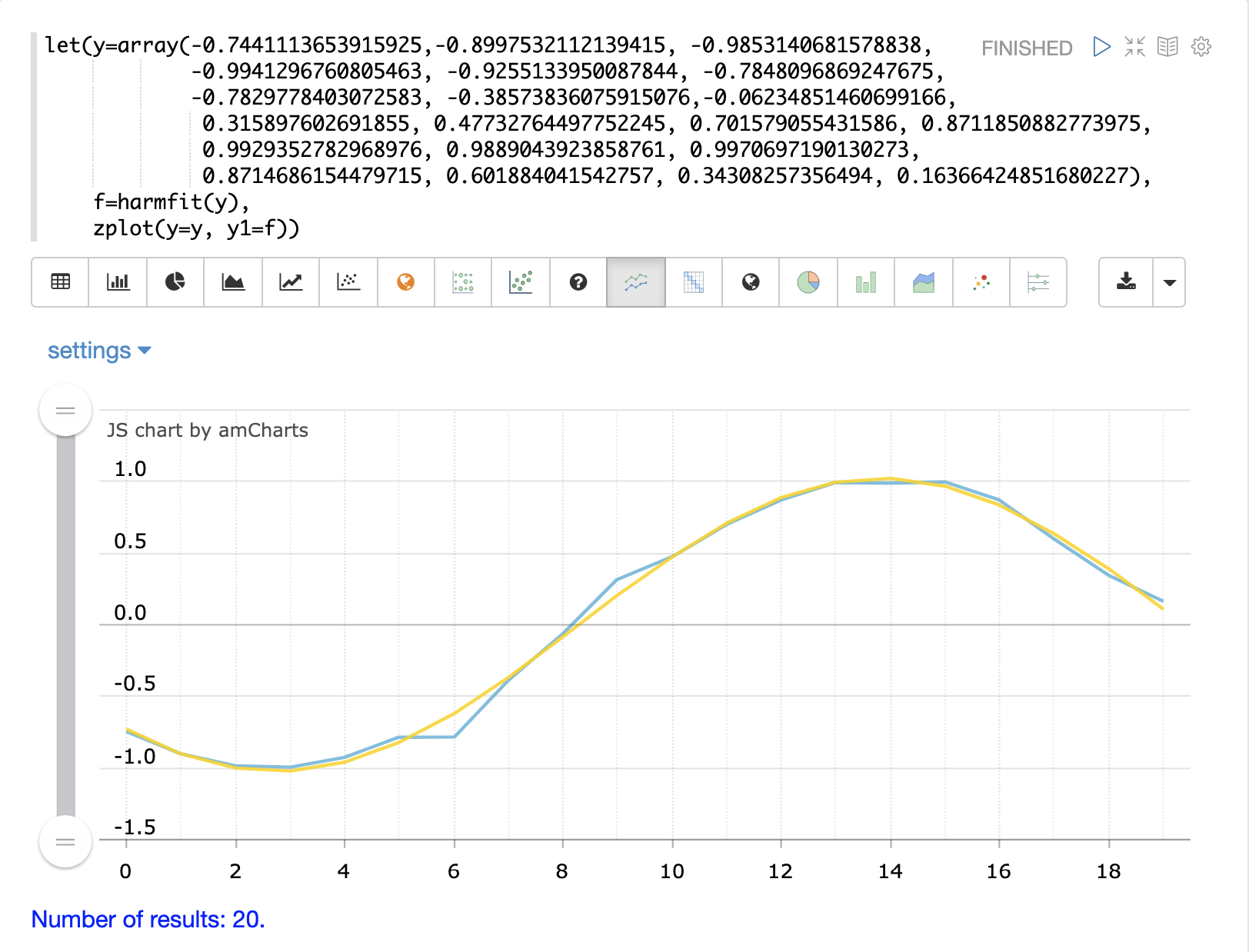
下面的範例顯示 harmfit 擬合正弦波的單一振盪。harmfit 函數會返回每個控制點的平滑值。傳回值也是一個模型，可供 predict、derivative 和 integrate 函數使用。

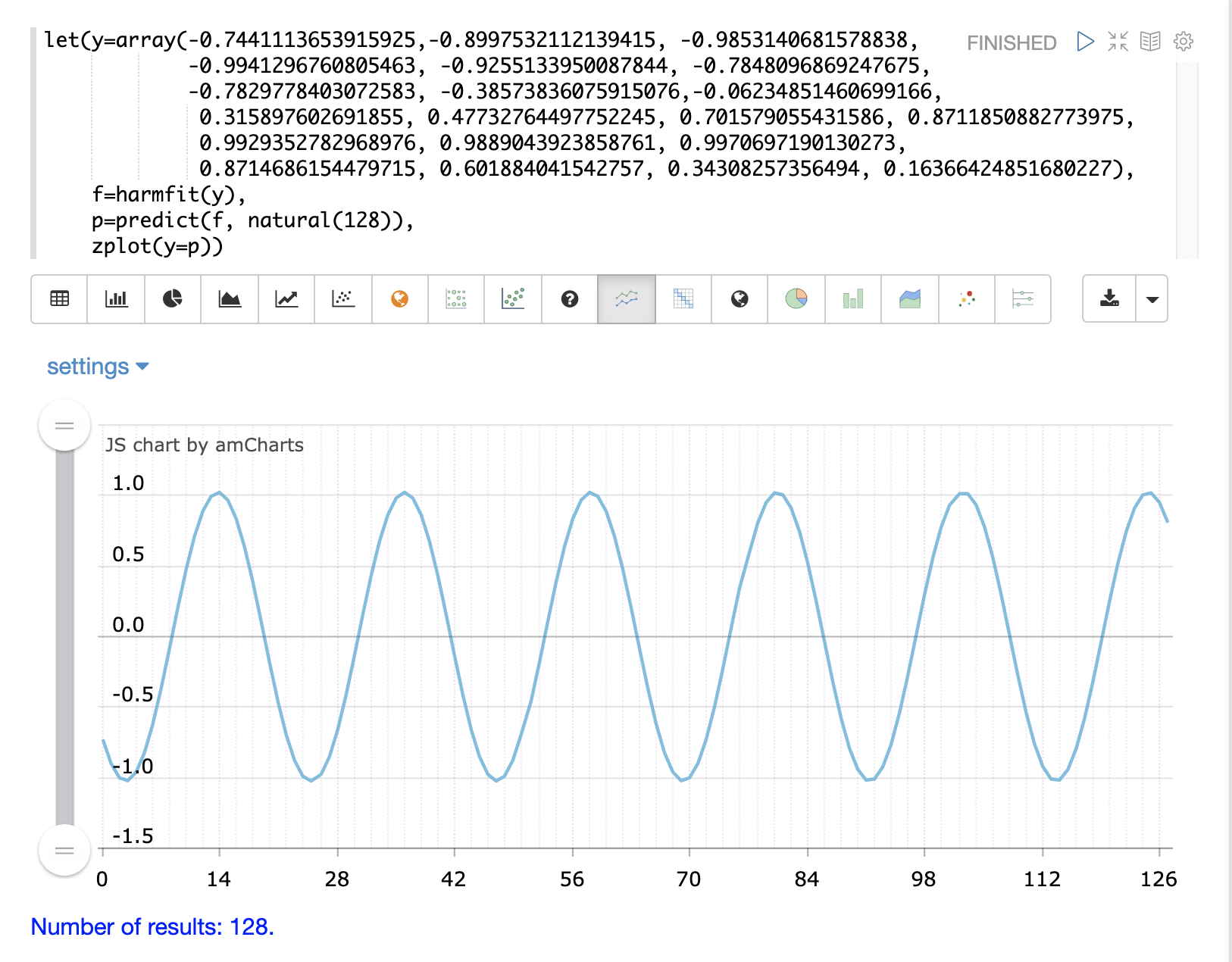
在下面的範例中，原始控制點以藍色顯示，而擬合的曲線以黃色顯示。

harmfit 的輸出是一個模型，可供 predict 函數使用來內插和外推正弦波。在下面的範例中，natural 函數會建立一個從 0 到 127 的 x 軸，用於預測模型的結果。這會將正弦波外推到 128 個點，而原始模型曲線只有 19 個控制點。