蒙地卡羅模擬
蒙地卡羅模擬通常用於模擬隨機(隨機)系統的行為。本使用者指南的這一節涵蓋了使用數學運算式執行蒙地卡羅模擬的基本知識。
隨機時間序列
股票價格的每日變動通常被描述為「隨機漫步」。但這到底是什麼意思,它與隨機時間序列有何不同?下面的範例將使用蒙地卡羅模擬來探索「隨機漫步」和隨機時間序列。
了解差異的一個有用的第一步是將每日股票報酬(計算為收盤價減去開盤價)視覺化為時間序列。
下面的範例使用 search 函數來傳回股票代碼 CVX (雪佛龍) 的 1000 天每日股票報酬。然後將 change_d 欄位(即當天的價格變動)繪製為時間序列。
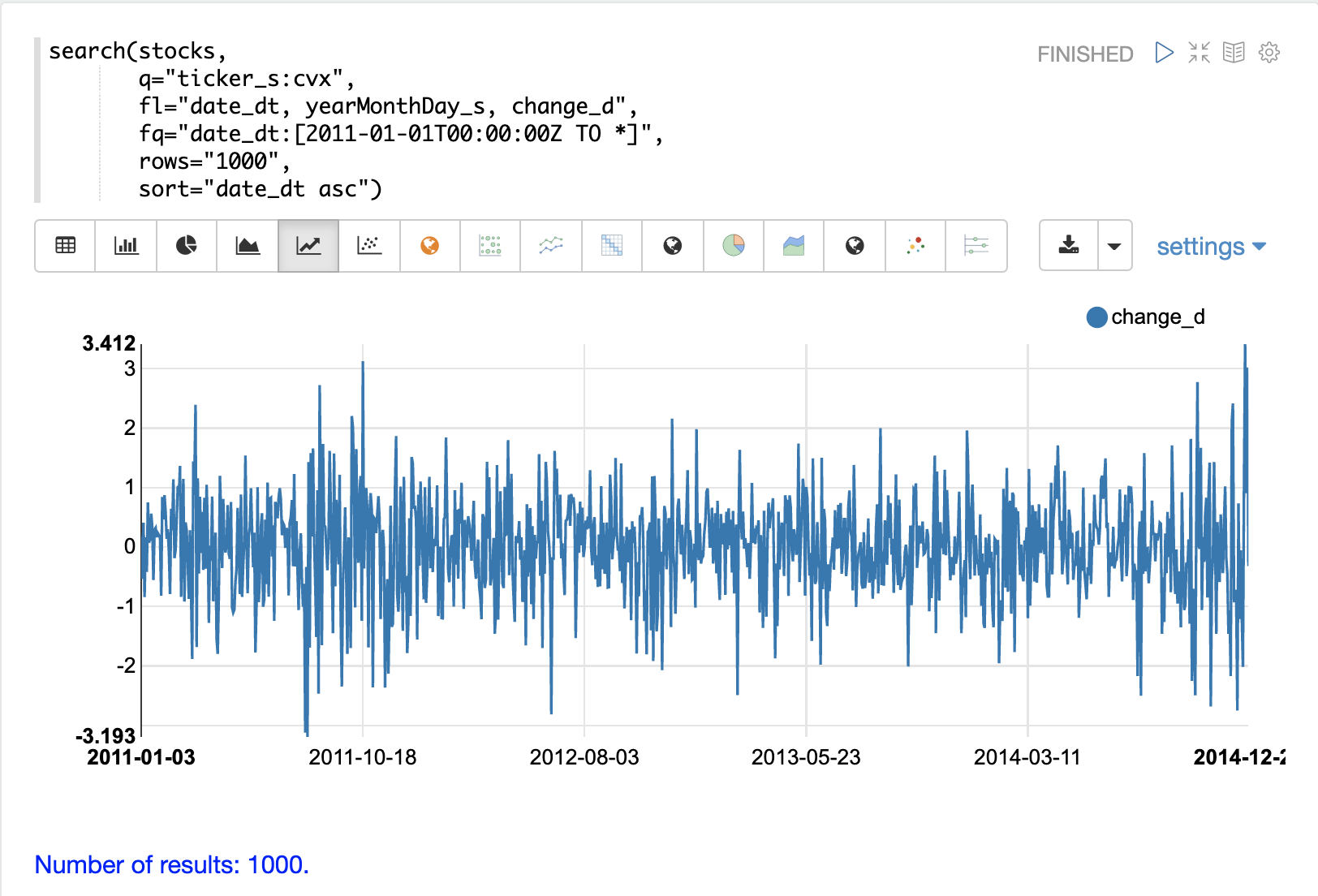
請注意,每日價格變動的時間序列在零以上和以下隨機移動。有些日子股票上漲,有些日子下跌,但步驟之間似乎沒有明顯的模式或任何依賴性。這暗示著這是一個隨機時間序列。
自相關
自相關測量訊號與自身相關的程度。自相關可用於確定向量是否包含訊號,或者時間序列中的值之間是否存在依賴性。如果時間序列中沒有訊號並且值之間沒有依賴性,則時間序列是隨機的。
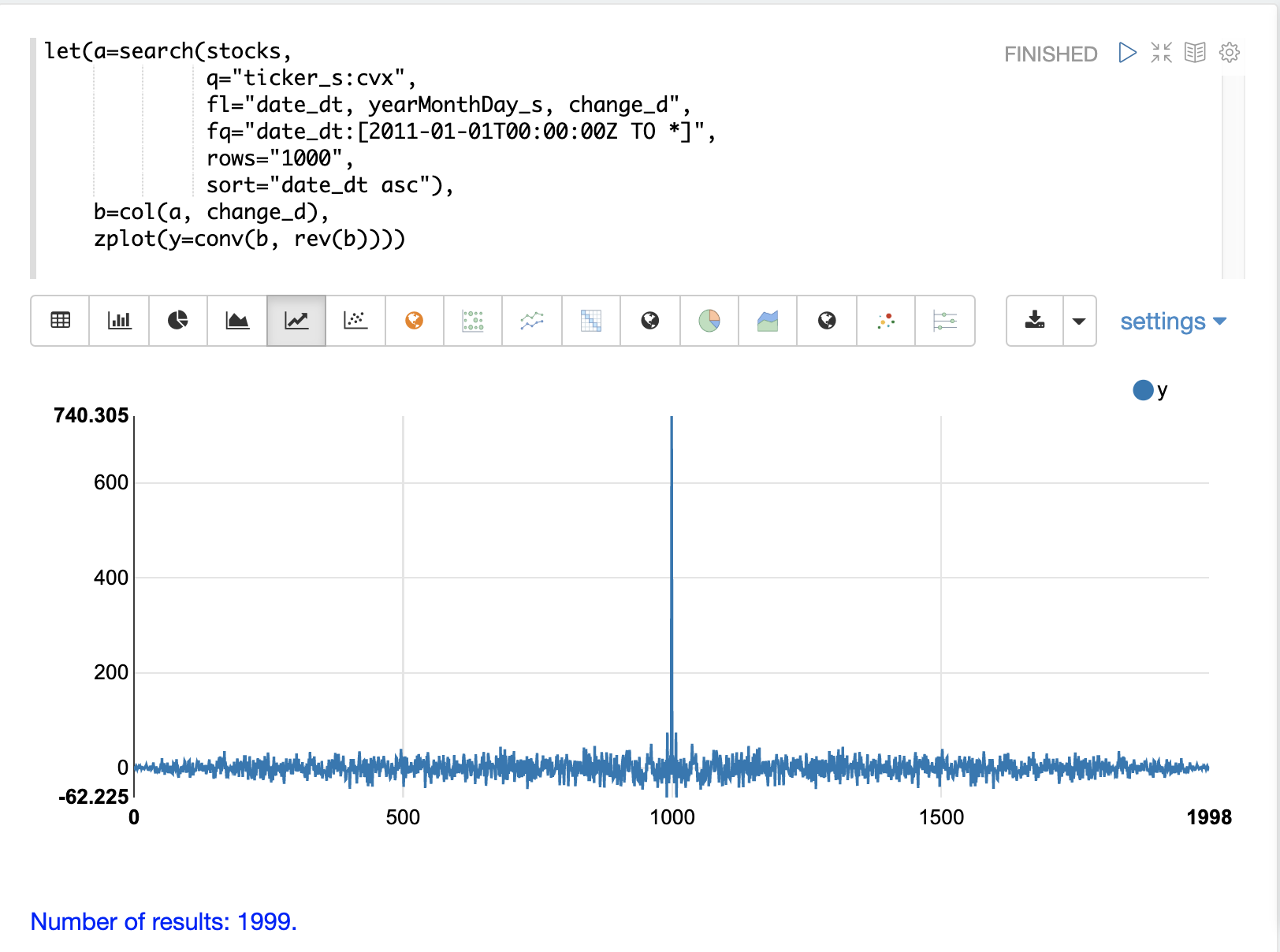
繪製 change_d 向量的自相關以確認它確實是隨機的很有用。
在以下範例中,搜尋結果會設定為一個變數,然後將 change_d 欄位向量化並儲存在變數 b 中。接著,使用 conv (卷積) 函數來自動關聯 change_d 向量。請注意,conv 函數只是將 change_d 向量與其反向副本「卷積」。這是使用卷積執行自動關聯的技術。使用者指南的 數位訊號處理 章節詳細介紹了卷積和自動關聯。在本節中,我們只會討論繪圖。
該圖顯示了相關性的強度,這是透過 conv 函數將 change_d 向量滑過自身時計算出來的。請注意,在圖中,有一段長時間的低強度相關性,看起來是隨機的。然後在中心出現一個高強度相關性的峰值,這是向量直接對齊的地方。接著是另一段長時間的低強度相關性。
這是純雜訊的自動關聯圖。每日股價變動似乎是隨機的時間序列。
視覺化分佈
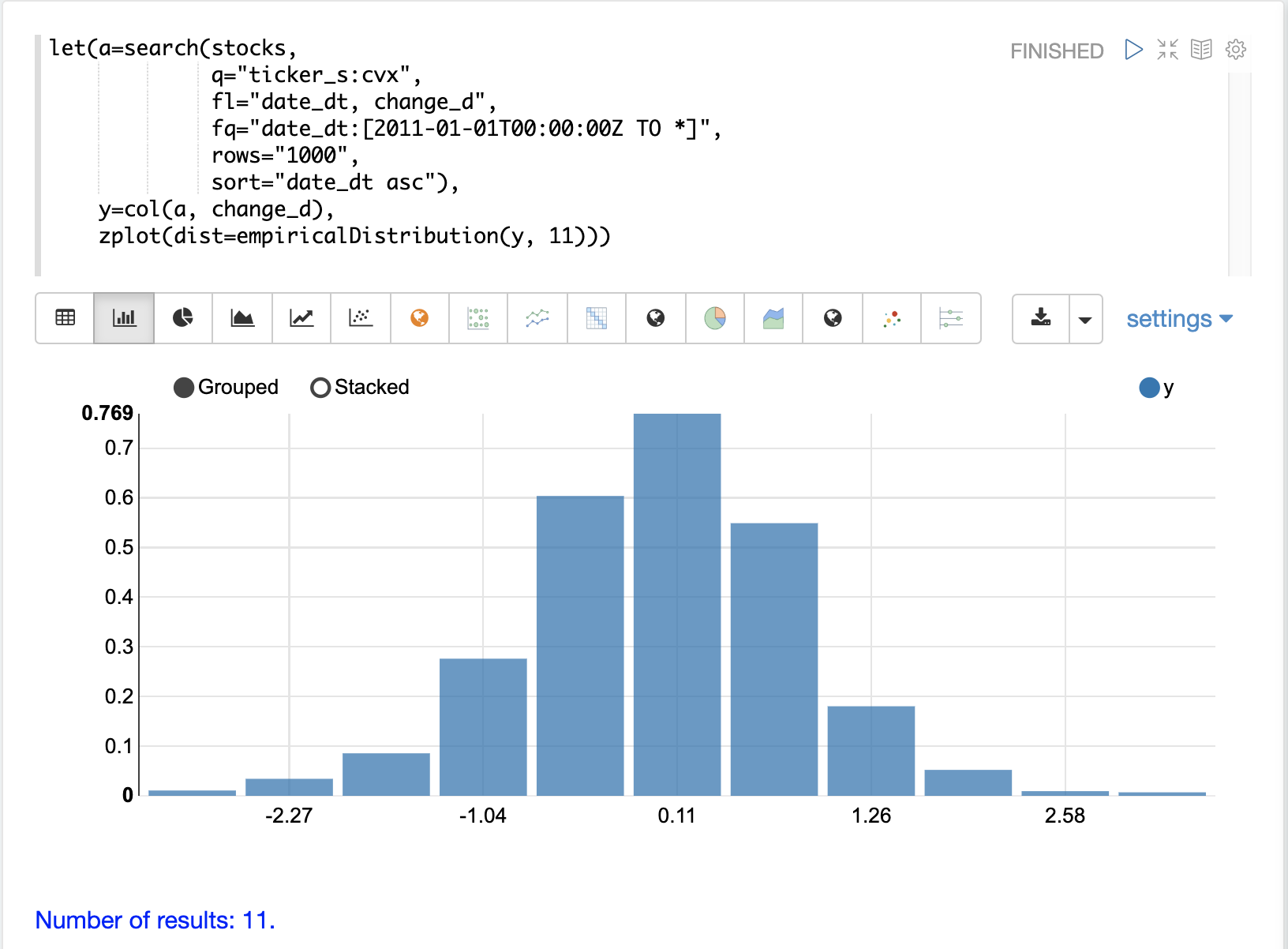
每日股價的隨機變化無法預測,但可以使用機率分佈來建模。為了對時間序列進行建模,我們將從視覺化 change_d 向量的分佈開始。在以下範例中,使用 empiricalDistribution 函數繪製 change_d 向量,以建立資料的 11 個區間的直方圖。請注意,該分佈似乎是常態分佈。每日股價變動往往會呈現常態分佈,儘管選擇 CVX 作為此範例的特定原因正是由於此特性。
擬合分佈
可以使用 ks 檢定來確定資料向量的分佈是否符合參考分佈。在以下範例中,使用 change_d 向量的平均值 (mean) 和標準差 (stddev) 作為參考分佈,對常態分佈執行 ks 檢定。ks 檢定正在檢查參考分佈與 change_d 向量本身,以查看它是否符合常態分佈。
請注意,在以下範例中,ks 檢定報告的 p 值為 .16278。通常使用 .05 或更低的 p 值來使檢定的虛無假設無效,該虛無假設是向量可能來自參考分佈。
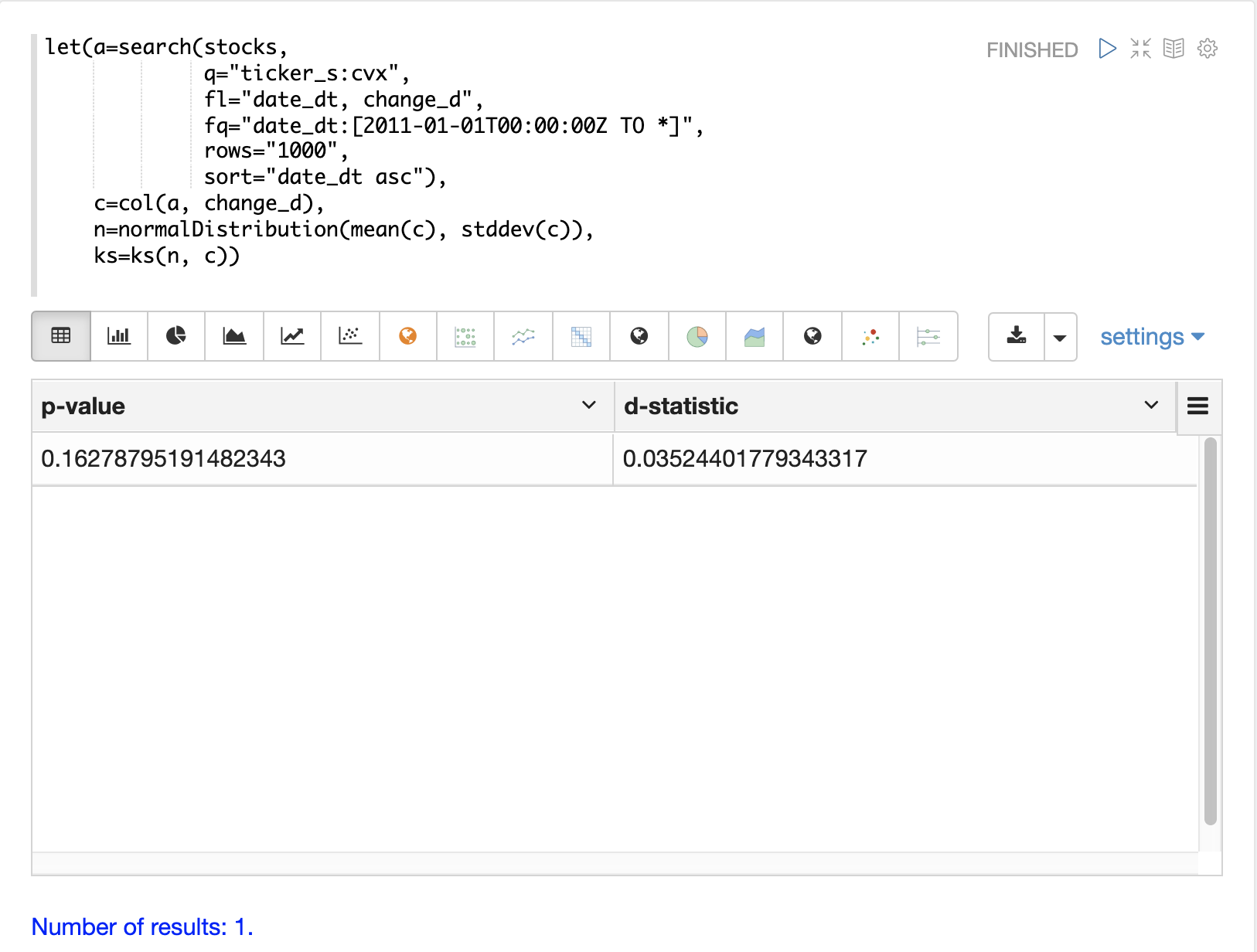
ks 檢定(往往相當敏感)已確認看起來是常態的視覺化結果。因此,將使用 change_d 向量的平均值和標準差的常態分佈來表示以下蒙地卡羅模擬中 Chevron 的每日股票報酬率。
蒙地卡羅
現在我們已經將分佈擬合到每日股票報酬率資料,我們可以使用 monteCarlo 函數來執行使用該分佈的模擬。
monteCarlo 函數會執行指定的次數。在每次執行時,它會設定一系列變數,並執行一個最終函數,該函數會傳回單一數值。monteCarlo 函數會將每次執行的結果收集到向量中並傳回。最終函數通常有一個或多個變數,這些變數在每次執行時會從機率分佈中抽取。sample 函數用於抽取樣本。
然後,可以將模擬的結果陣列視為經驗分佈,以了解模擬結果的機率。
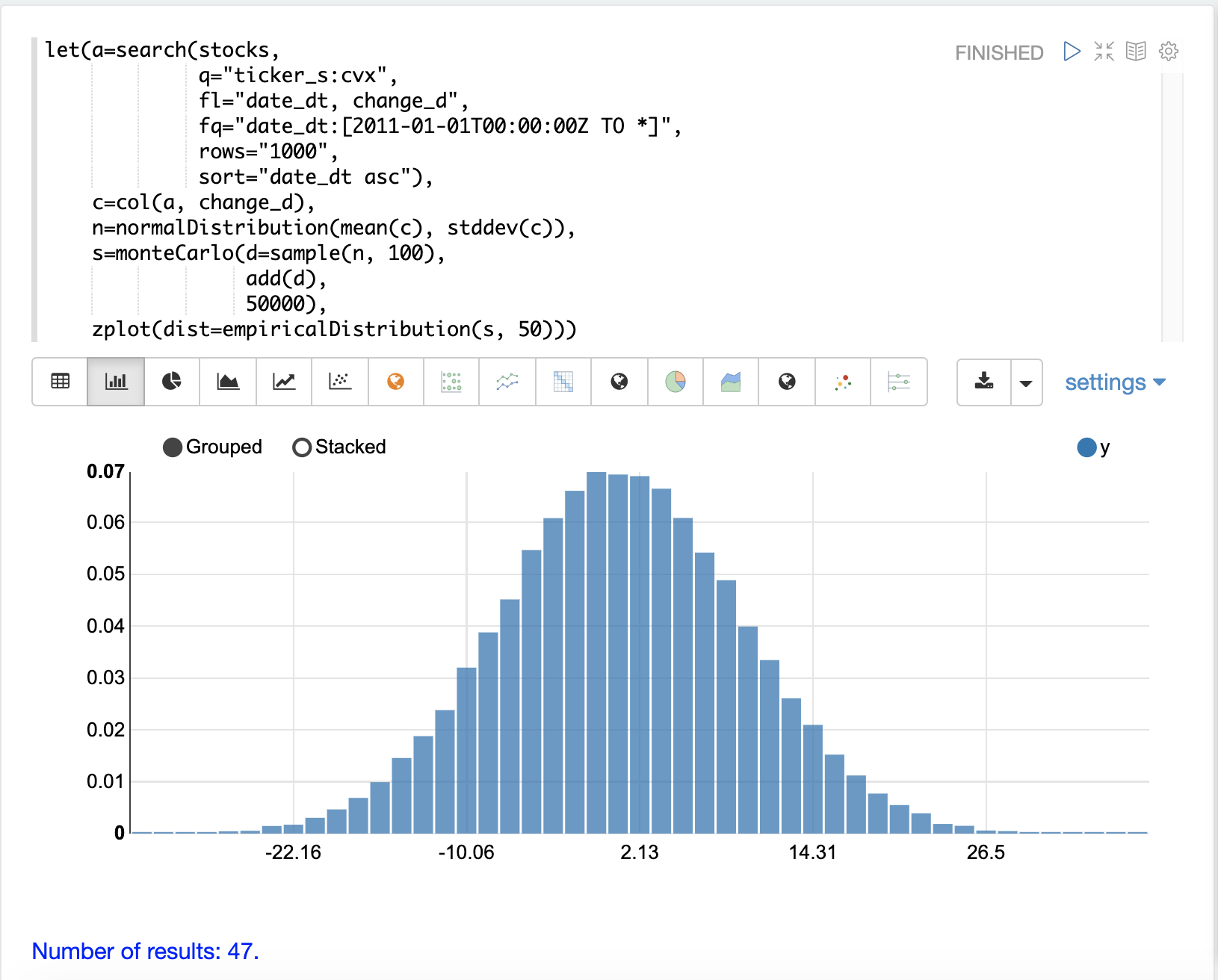
以下範例使用 monteCarlo 函數來模擬 100 天股票報酬率總額的分佈。
在範例中,從 change_d 向量的平均值和標準差建立 normalDistribution。然後,monteCarlo 函數從常態分佈中抽取 100 個樣本,以代表 100 天的股票報酬率,並將樣本向量設定為變數 d。
然後,add 函數計算 100 天樣本的總報酬率。add 函數的輸出會由 monteCarlo 函數收集。此過程重複 50000 次,每次執行都會從常態分佈中抽取不同的樣本集。
模擬的結果會設定為變數 s,其中包含 50000 次執行的總報酬率。
然後,使用 empiricalDistribution 函數將模擬的輸出視覺化為 50 個區間的直方圖。該分佈視覺化了股票代碼 CVX 100 天股票報酬率不同總報酬率的機率。
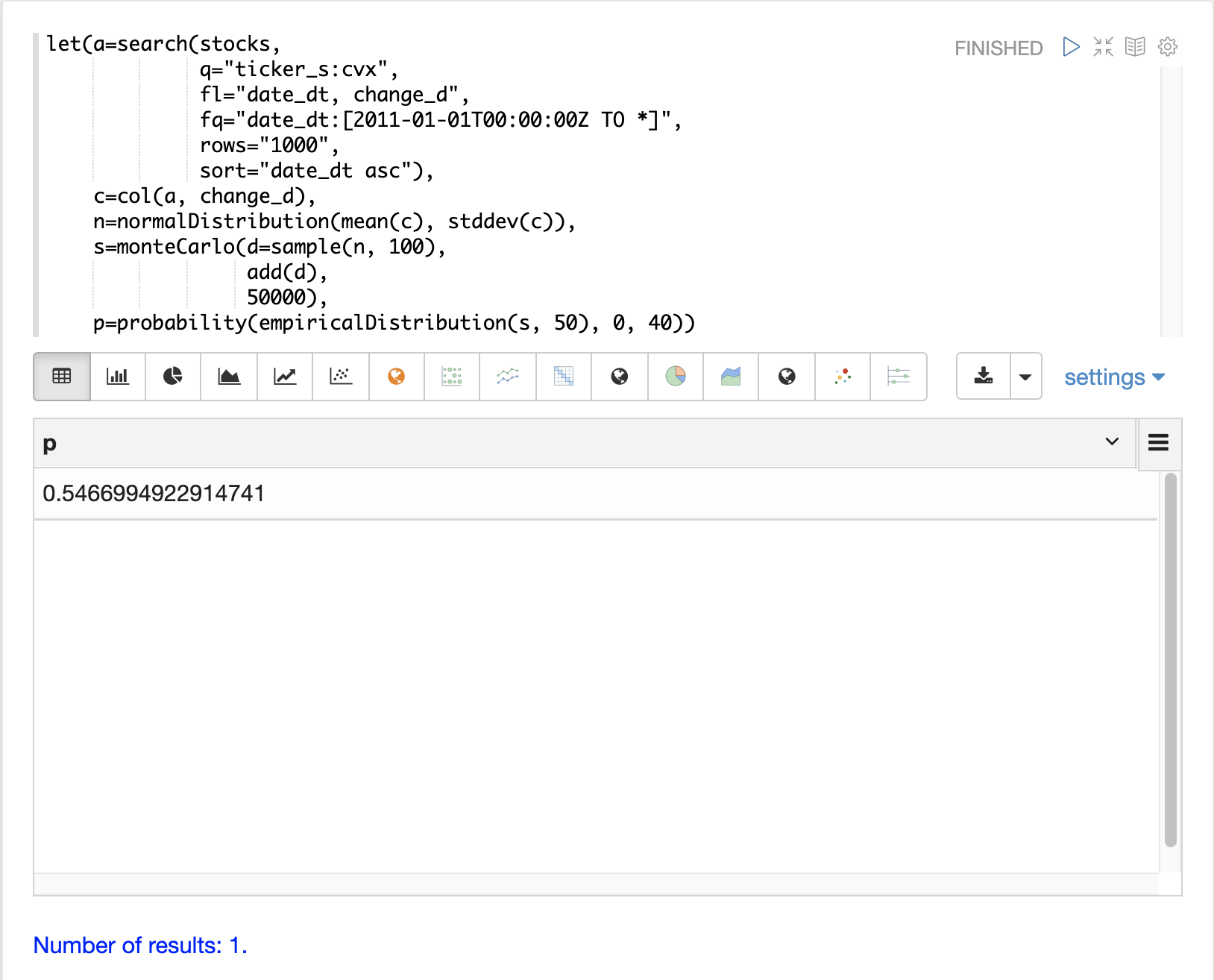
然後,可以使用 probability 和 cumulativeProbability 函數來了解有關 empiricalDistribution 的更多資訊。例如,可以使用 probability 函數來計算 100 天股票報酬率的非負報酬率的機率。
以下範例使用 probability 函數從模擬的 empiricalDistribution 中傳回 0 到 40 範圍內的報酬率機率。
隨機漫步
monteCarlo 函數也可以用於從每日股票報酬率的 normalDistribution 中模擬每日股價的隨機漫步。隨機漫步是一個時間序列,其中每一步都是透過將隨機樣本新增到前一步驟來計算的。這會建立一個時間序列,其中每個值都取決於前一個值,這模擬了股價的自動關聯性。
在以下範例中,透過在每次蒙地卡羅迭代時將隨機樣本新增到變數 v 來實現隨機漫步。變數 v 會在迭代之間維護,因此每次迭代都會使用 v 的前一個值。double 函數是每次迭代執行的最終函數,它只是以雙精度值傳回 v 的值。此範例迭代 1000 次,以建立 1000 步的隨機漫步。
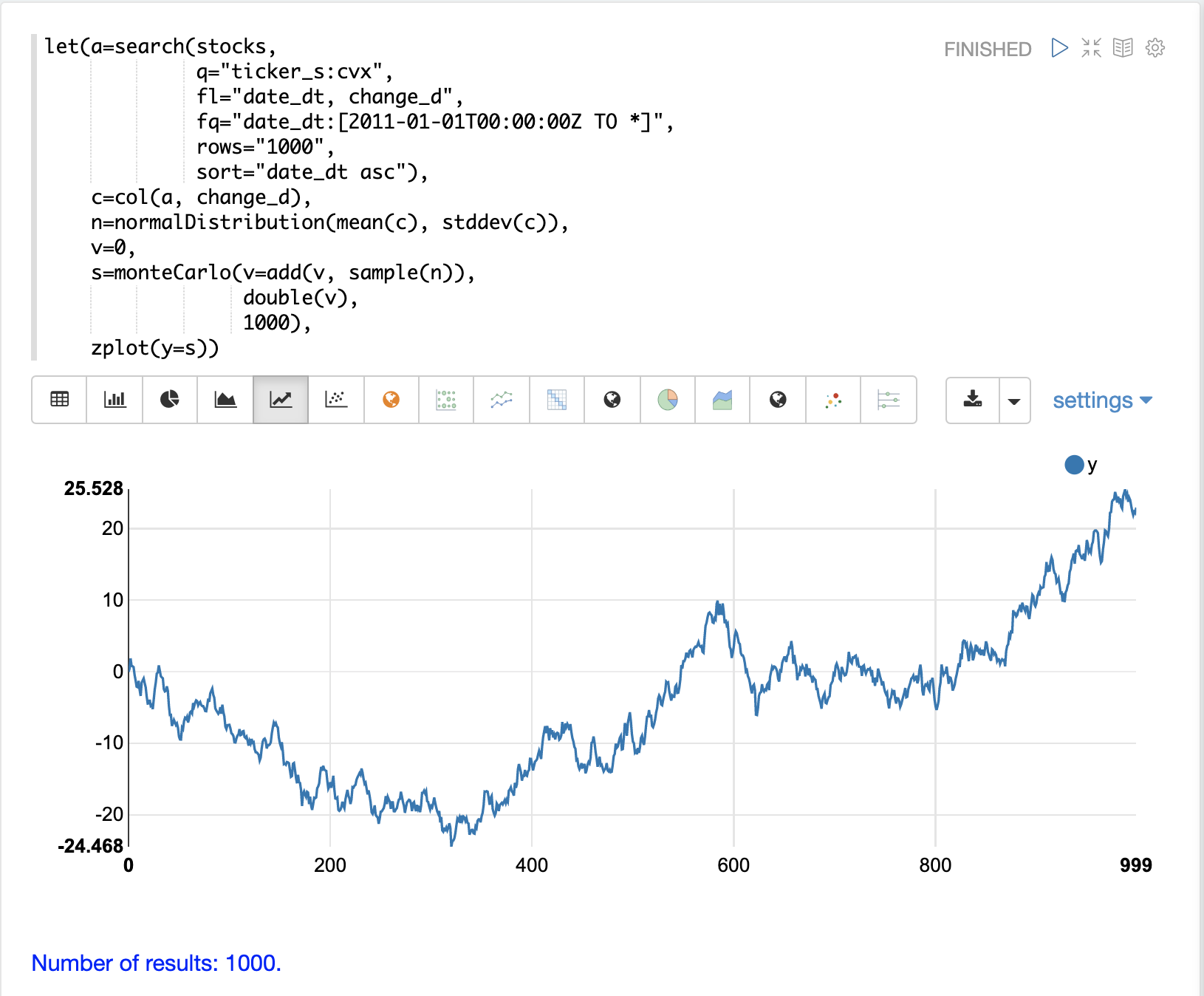
請注意,由於步驟之間的相依性而導致每日股價的自動關聯性所產生的圖與每日股價的隨機變化所產生的圖非常不同。
多變量常態分佈
multiVariateNormalDistribution 函數可用於對兩個或多個常態分佈的變數進行建模和模擬。它還將變數之間的相關性納入模型,這使得可以研究相關性如何影響可能的結果。
在以下範例中,探討了兩種股票的每日總報酬率的模擬。ALL 股票代碼 (Allstate) 與先前範例中的 CVX 股票代碼 (Chevron) 一起使用。
相關性和共變異數
多變量模擬顯示了相關性對可能結果的影響。在開始實際模擬之前,首先了解 Allstate 和 Chevron 股票報酬率之間的相關性和共變異數會很有幫助。
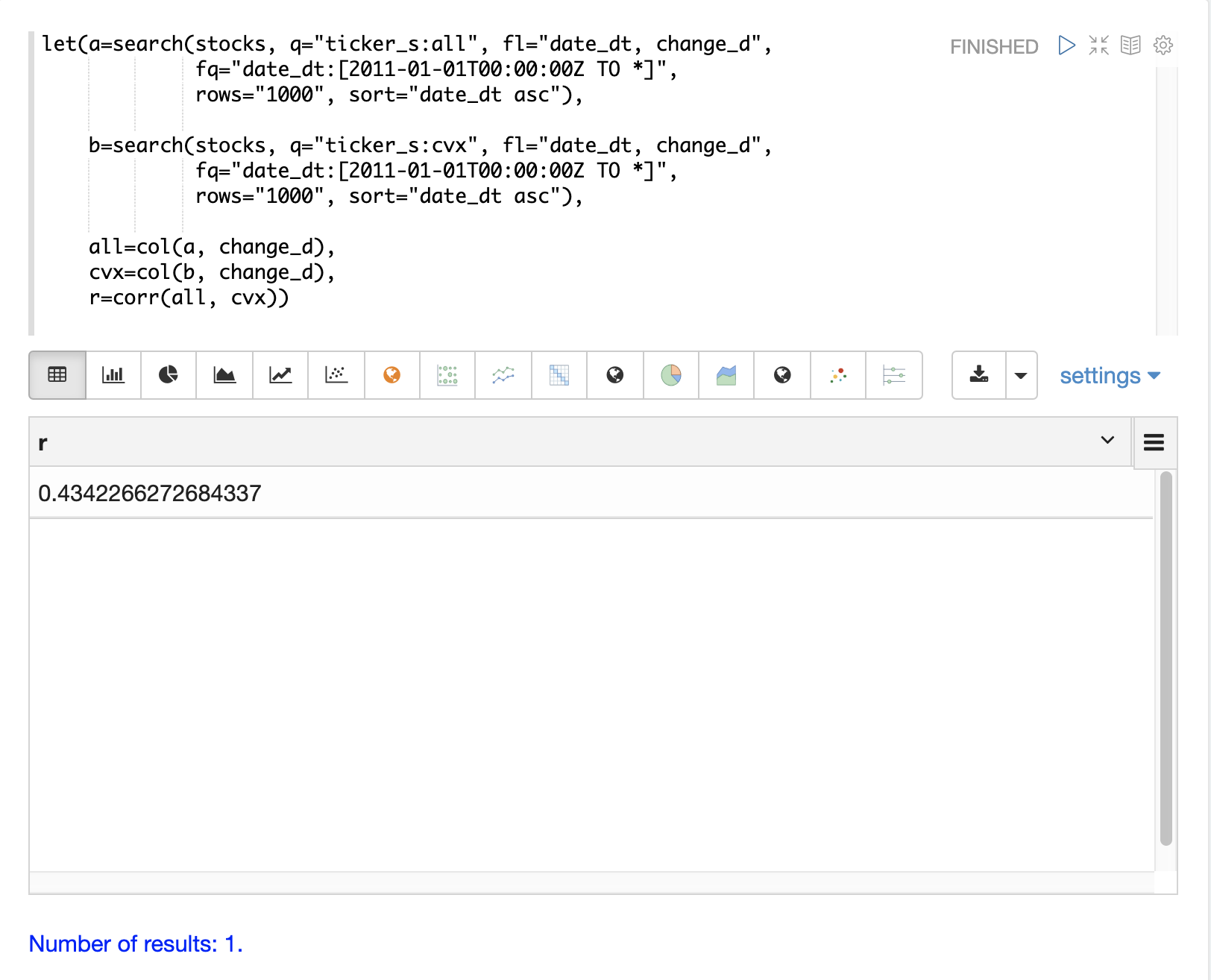
以下範例執行兩個搜尋來檢索所有 Allstate 和 Chevron 的每日股票報酬率。來自兩個報酬率的 change_d 向量會讀入變數 (all 和 cvx),並使用 corr 函數計算兩個向量的皮爾森相關性。
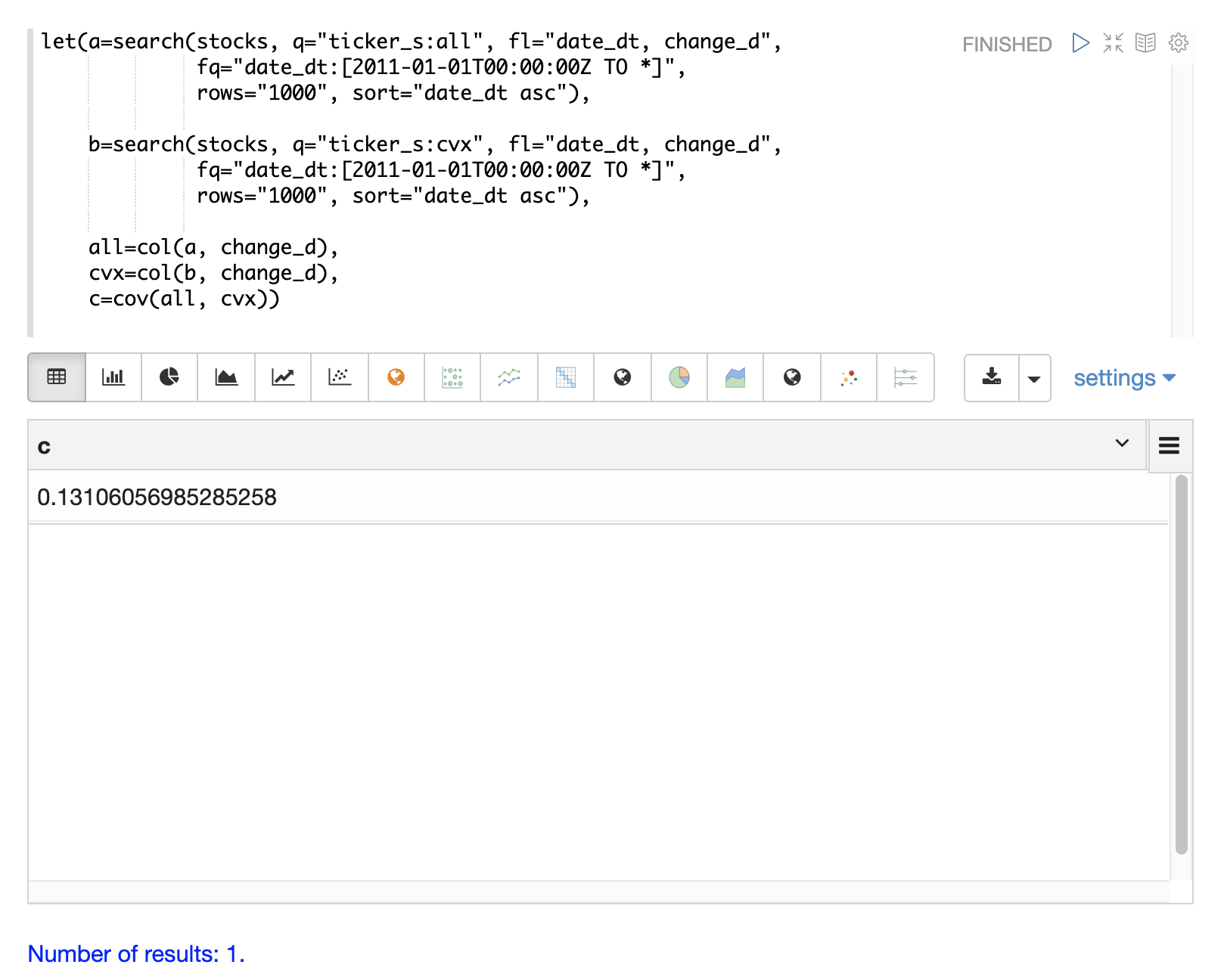
共變異數是未縮放的相關性度量。共變異數是多變量模擬所使用的度量,因此計算兩個股票報酬率的共變異數也很有用。以下範例會計算共變異數。
共變異數矩陣
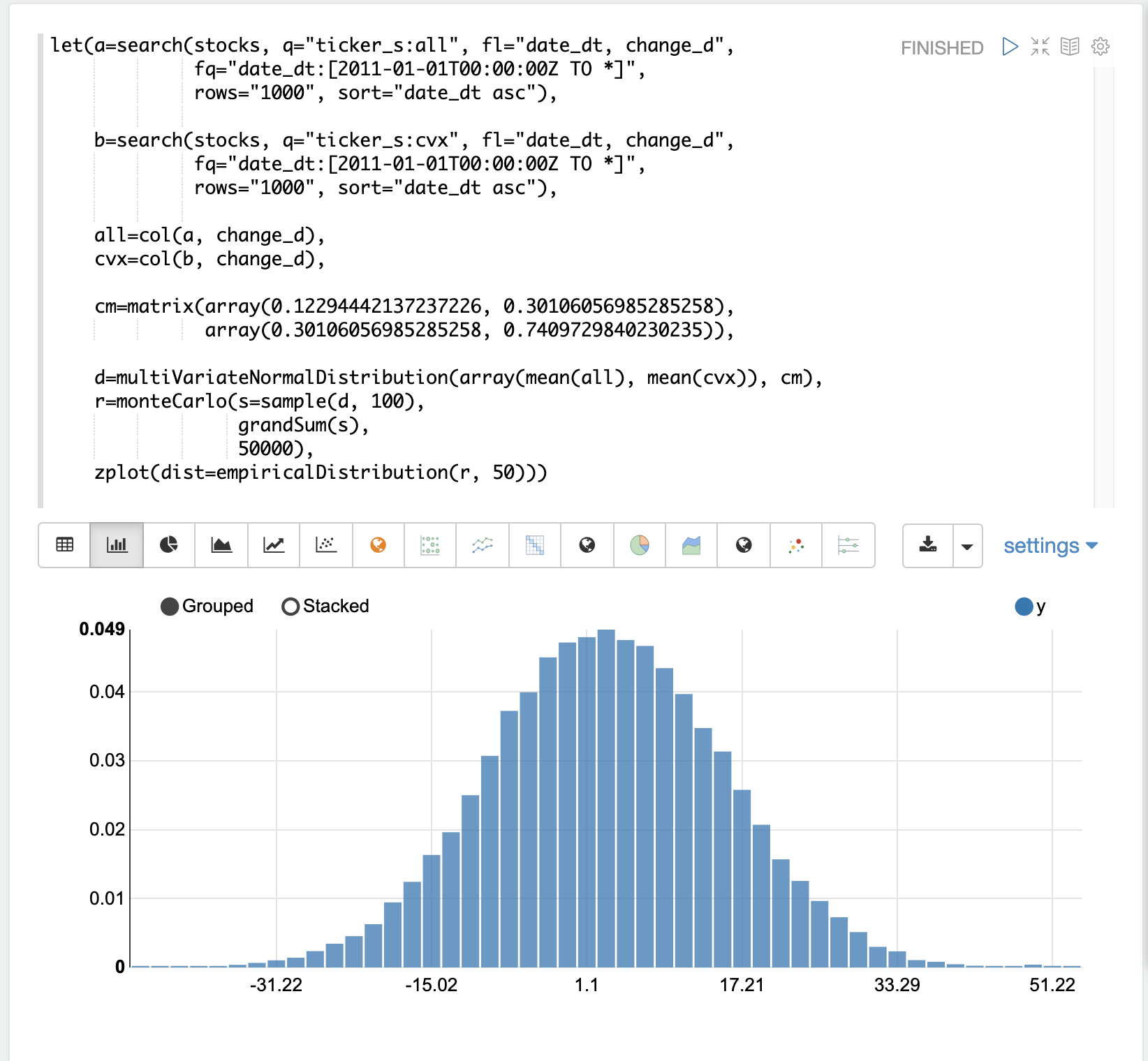
共變異數矩陣實際上是 multiVariateNormalDistribution 所需的,因為它同時包含兩個股票報酬率向量的變異數和兩個向量之間的共變異數。cov 函數會計算矩陣各列的共變異數矩陣。
以下範例示範如何透過將 all 和 cvx 向量作為列新增到矩陣來計算共變異數矩陣。然後使用 transpose 函數轉置矩陣,使 all 向量成為第一列,而 cvx 向量成為第二列。
然後,cov 函數會計算矩陣各列的共變異數矩陣並傳回結果。
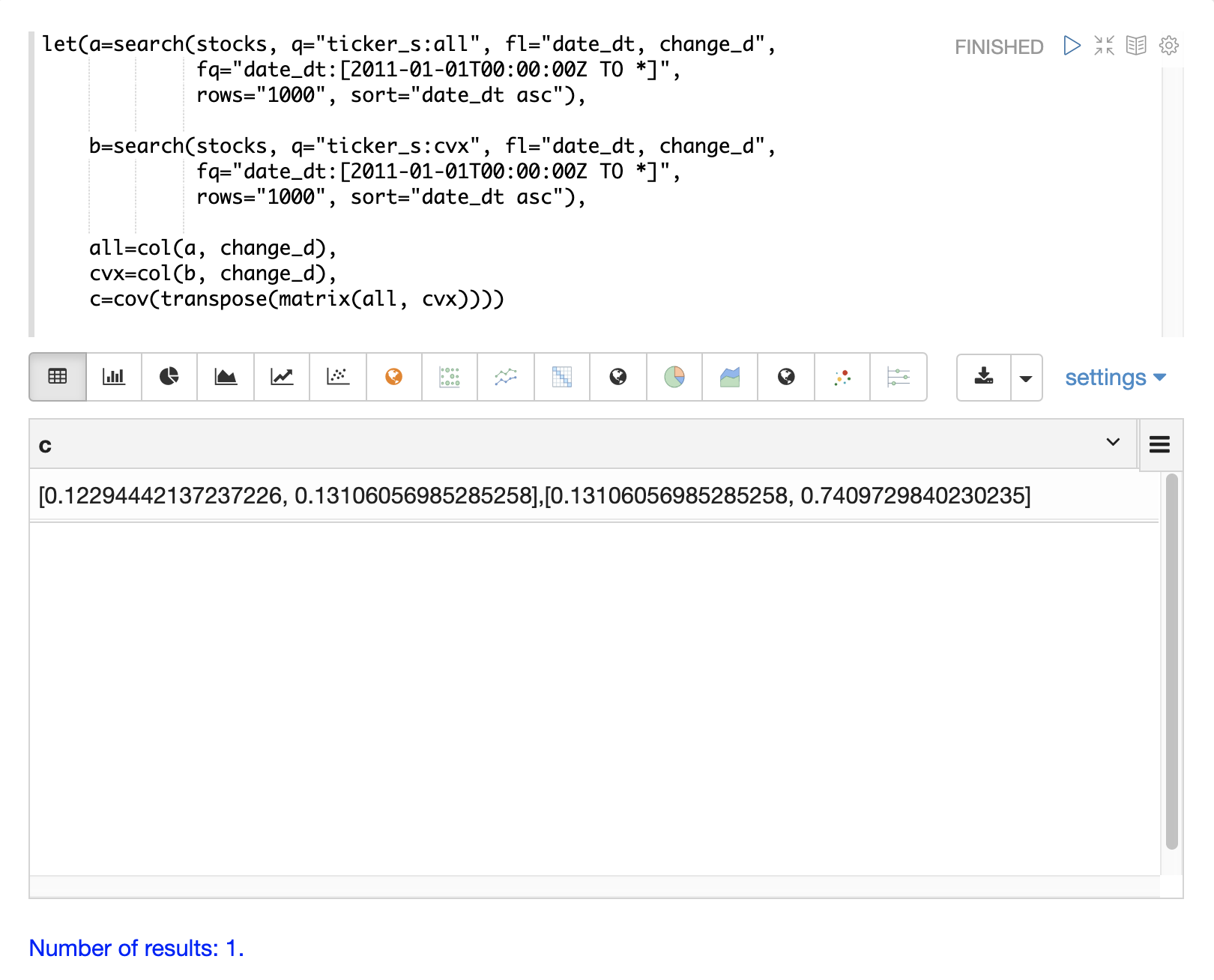
共變異數矩陣是一個方陣,其中包含每個向量的變異數和向量之間的共變異數,如下所示
all cvx
all [0.12294442137237226, 0.13106056985285258],
cvx [0.13106056985285258, 0.7409729840230235]多變量模擬
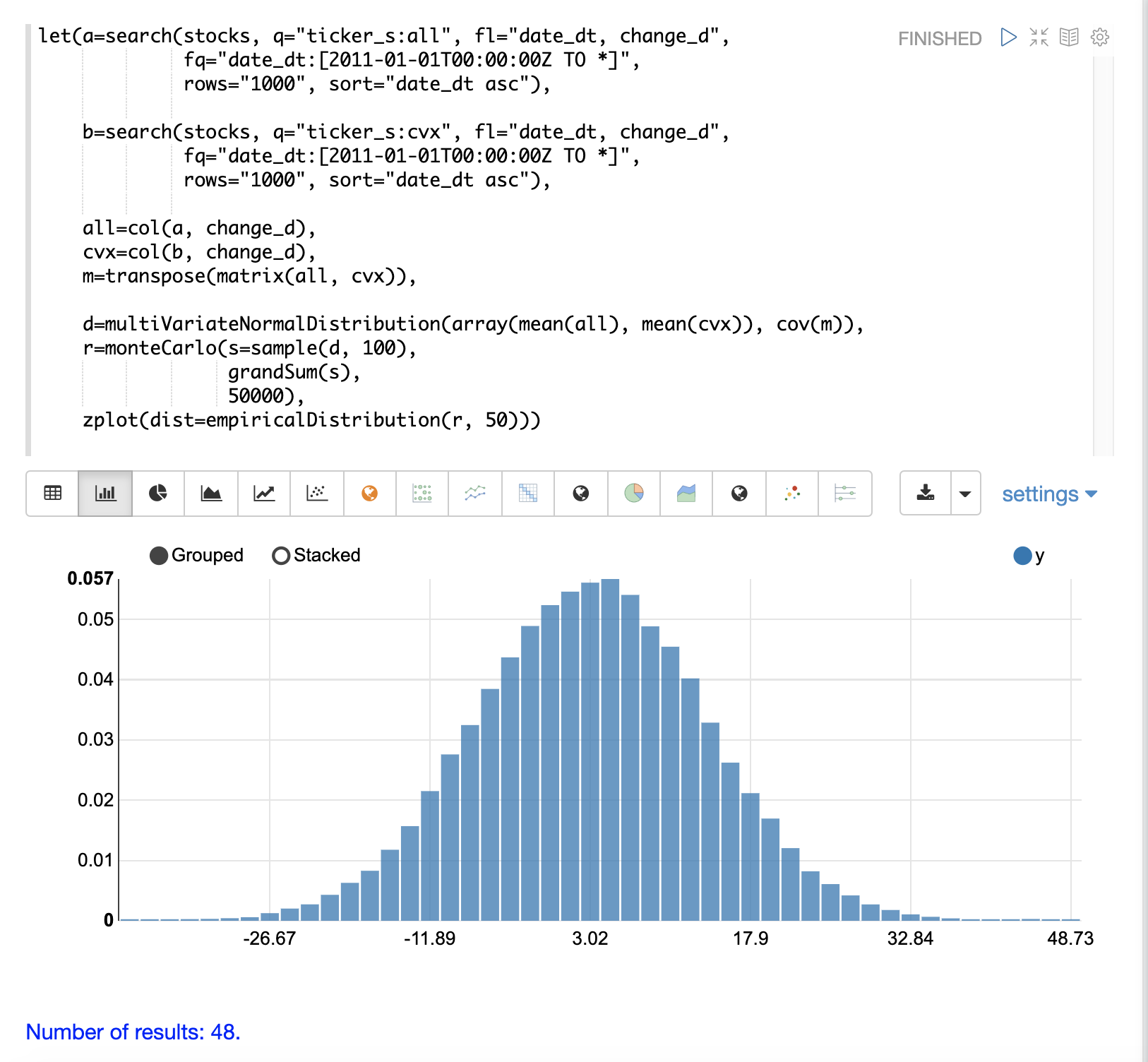
以下範例示範使用 multiVariateNormalDistribution 的兩個股票代碼的蒙地卡羅模擬。
在範例中,會檢索股票代碼 all (Allstate) 和 cvx (Chevron) 的 change_d 欄位結果集,並讀入向量中。
然後從兩個向量建立一個矩陣,並將其轉置,使矩陣包含兩列,其中一列包含 all 向量,另一列包含 cvx 向量。
然後,使用兩個參數建立 multiVariateNormalDistribution。第一個參數是 mean 值的陣列。在此範例中,為 all 向量和 cvx 向量的平均值。第二個參數是從兩個向量的雙列矩陣建立的共變異數矩陣。
然後,monteCarlo 函數透過在每次迭代時從 multiVariateNormalDistribution 中抽取 100 個樣本來執行模擬。每個樣本集都是一個具有 100 列和 2 列的矩陣,其中包含來自 all 和 cvx 分佈的股票報酬率樣本。列的分佈將與用於建立 multiVariateNormalDistribution 的常態分佈相符。樣本列的共變異數將與共變異數矩陣相符。
在每次迭代時,使用 grandSum 函數對樣本矩陣的所有值求和,以獲得兩種股票的總股票報酬率。
模擬的輸出是一個向量,其可以與單一股票代碼模擬完全相同的方式視為經驗分佈。在此範例中,它繪製為 50 個區間的直方圖,該直方圖視覺化了股票代碼 all 和 cvx 100 天股票報酬率不同總報酬率的機率。