機率分佈

本使用者指南章節涵蓋數學表示式程式庫中包含的機率分佈框架。

視覺化

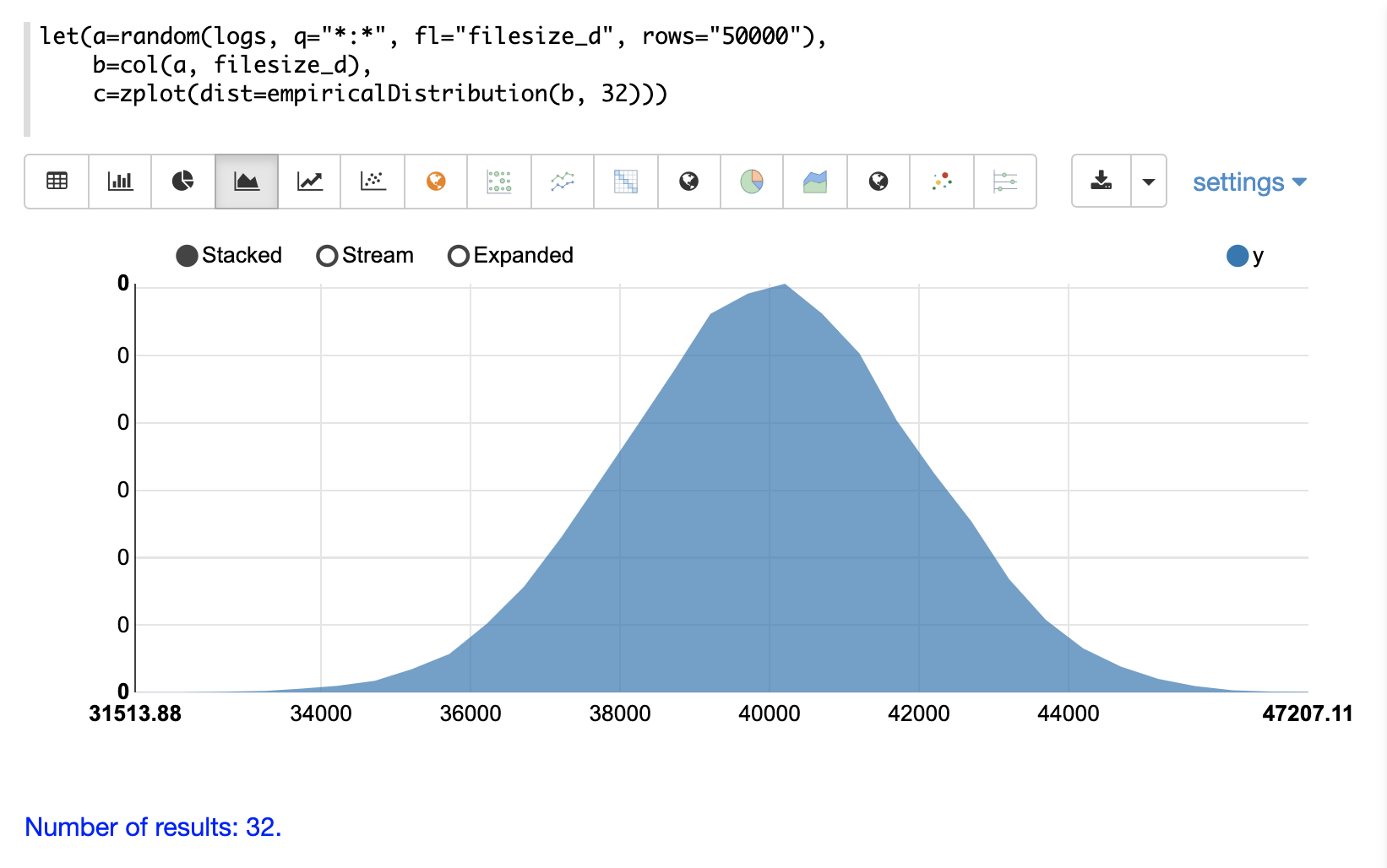
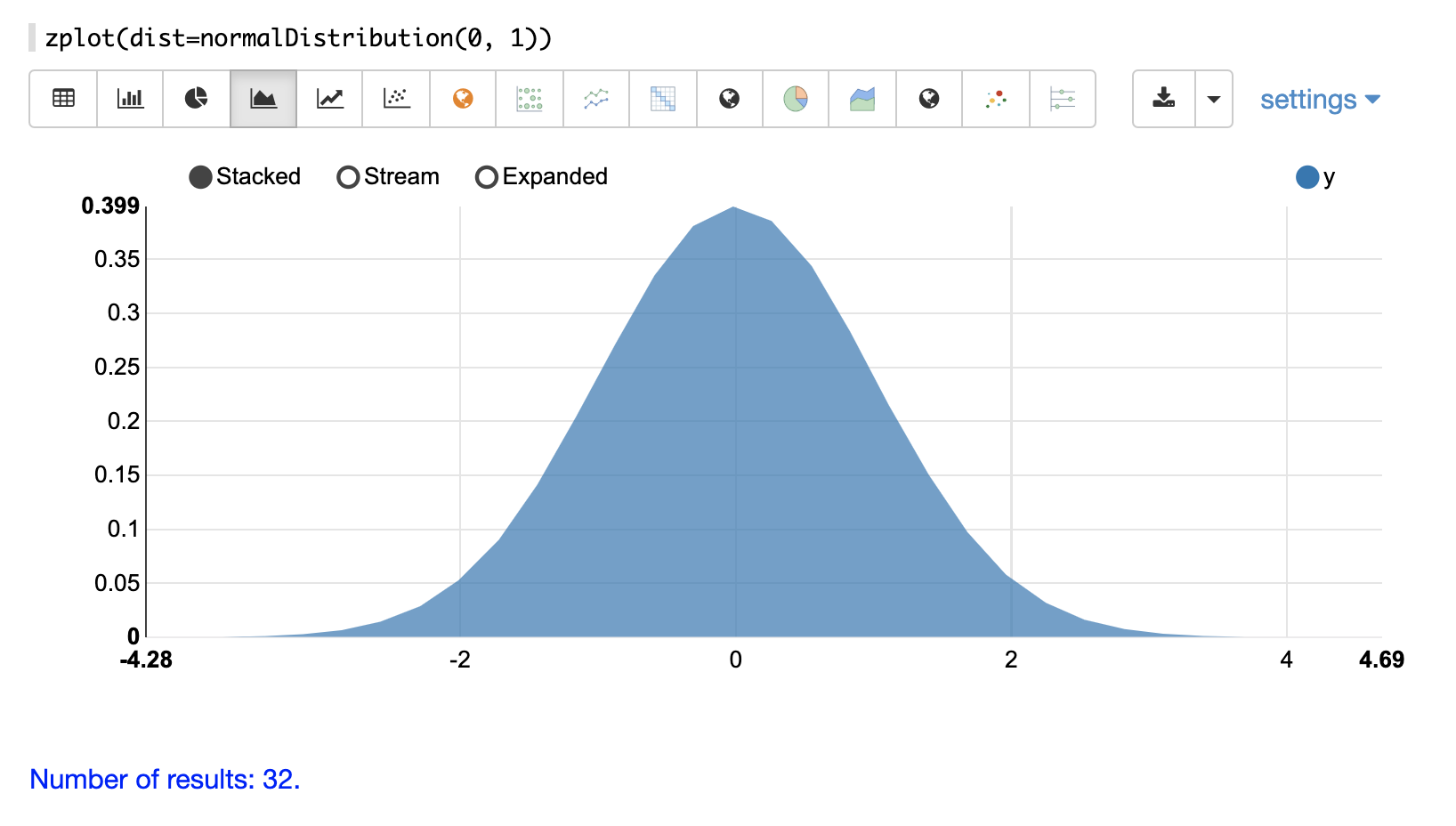
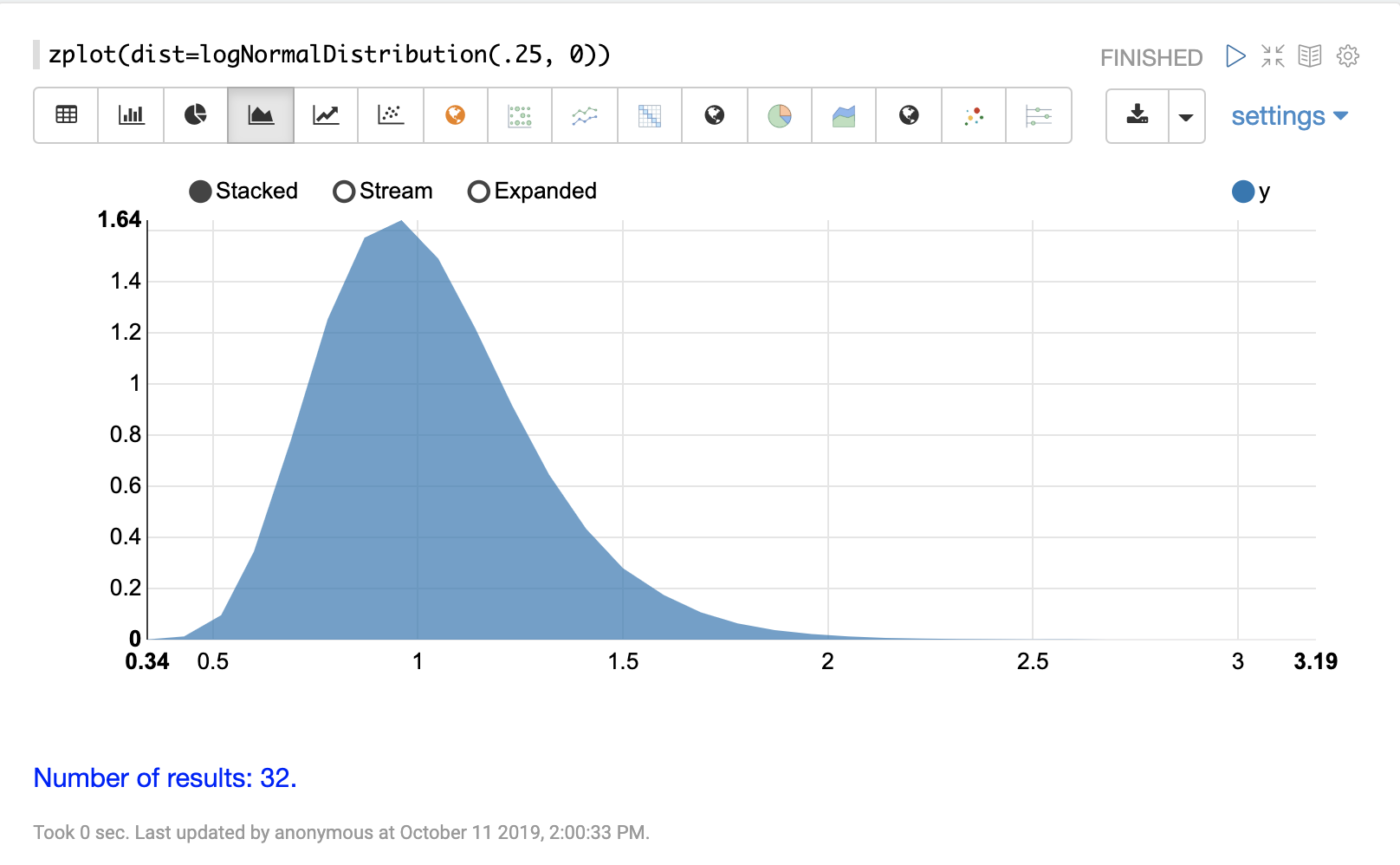
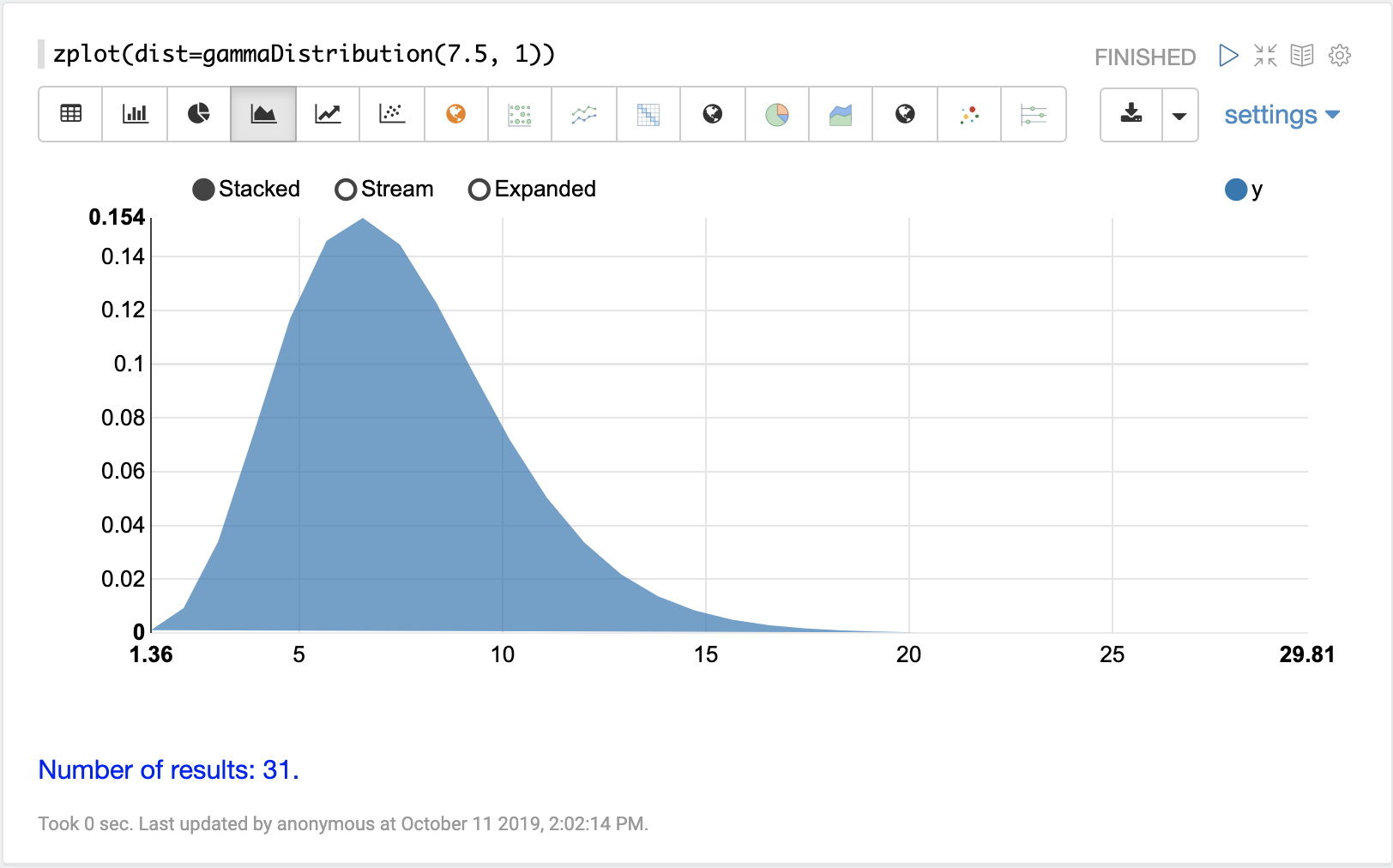
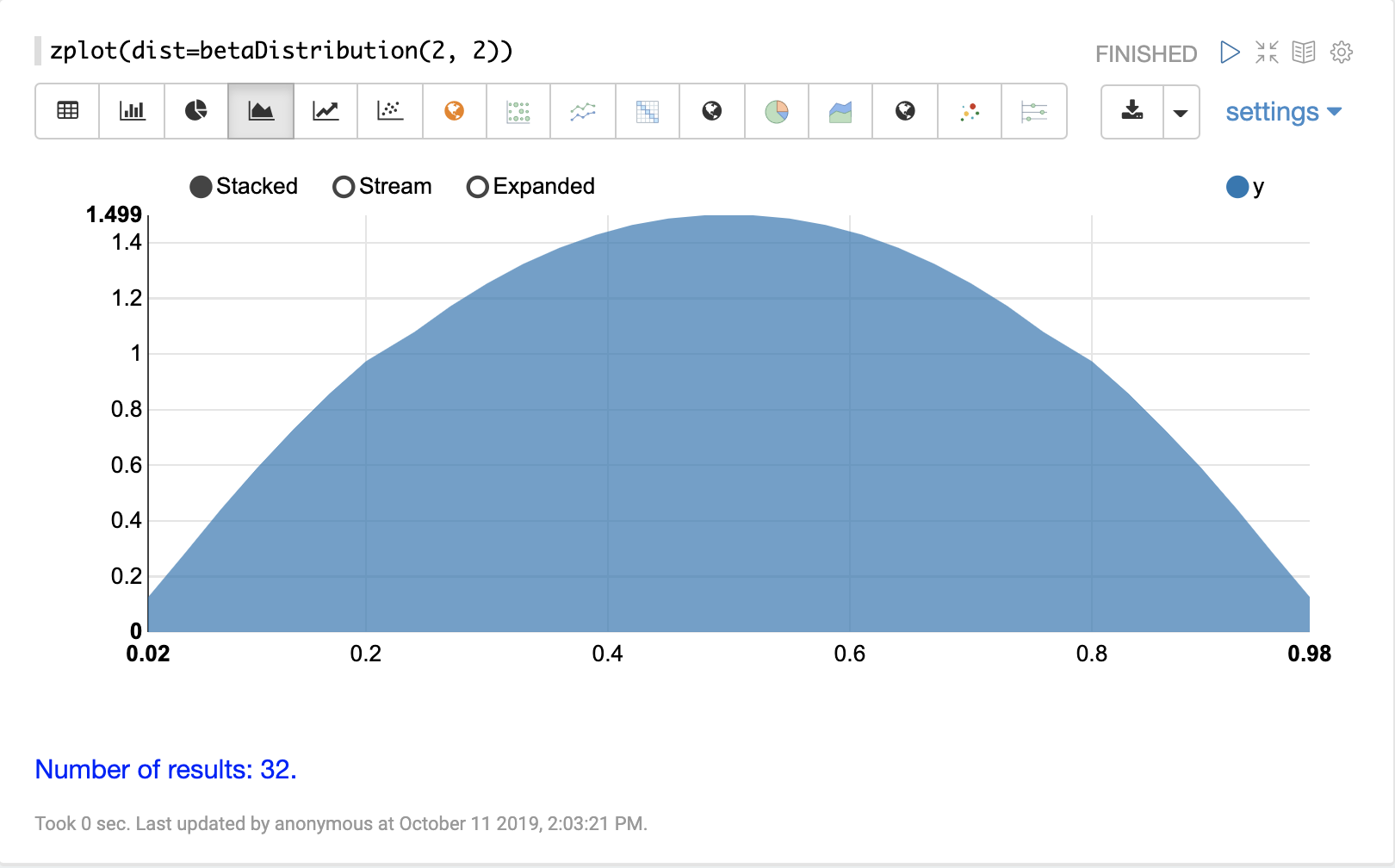
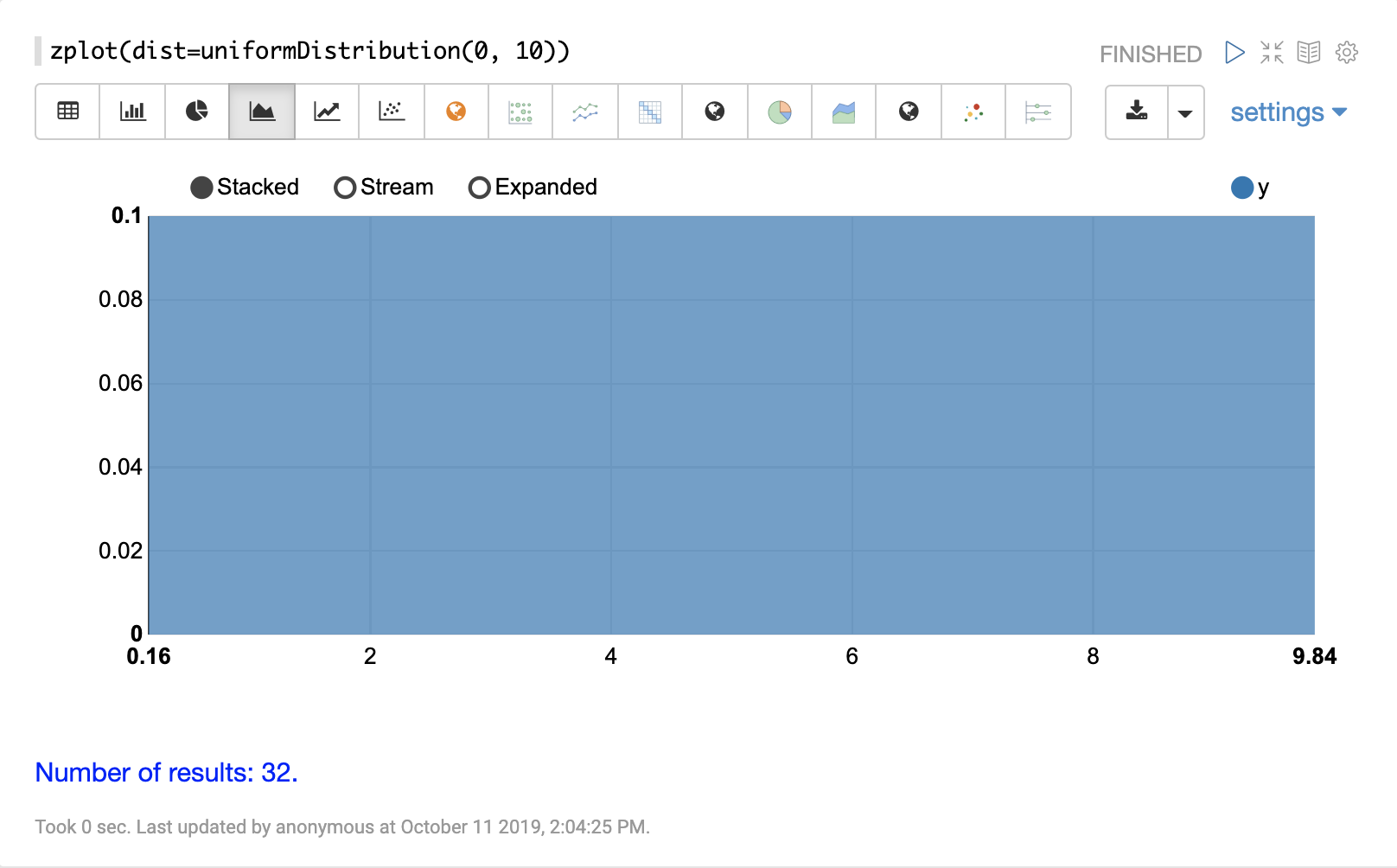
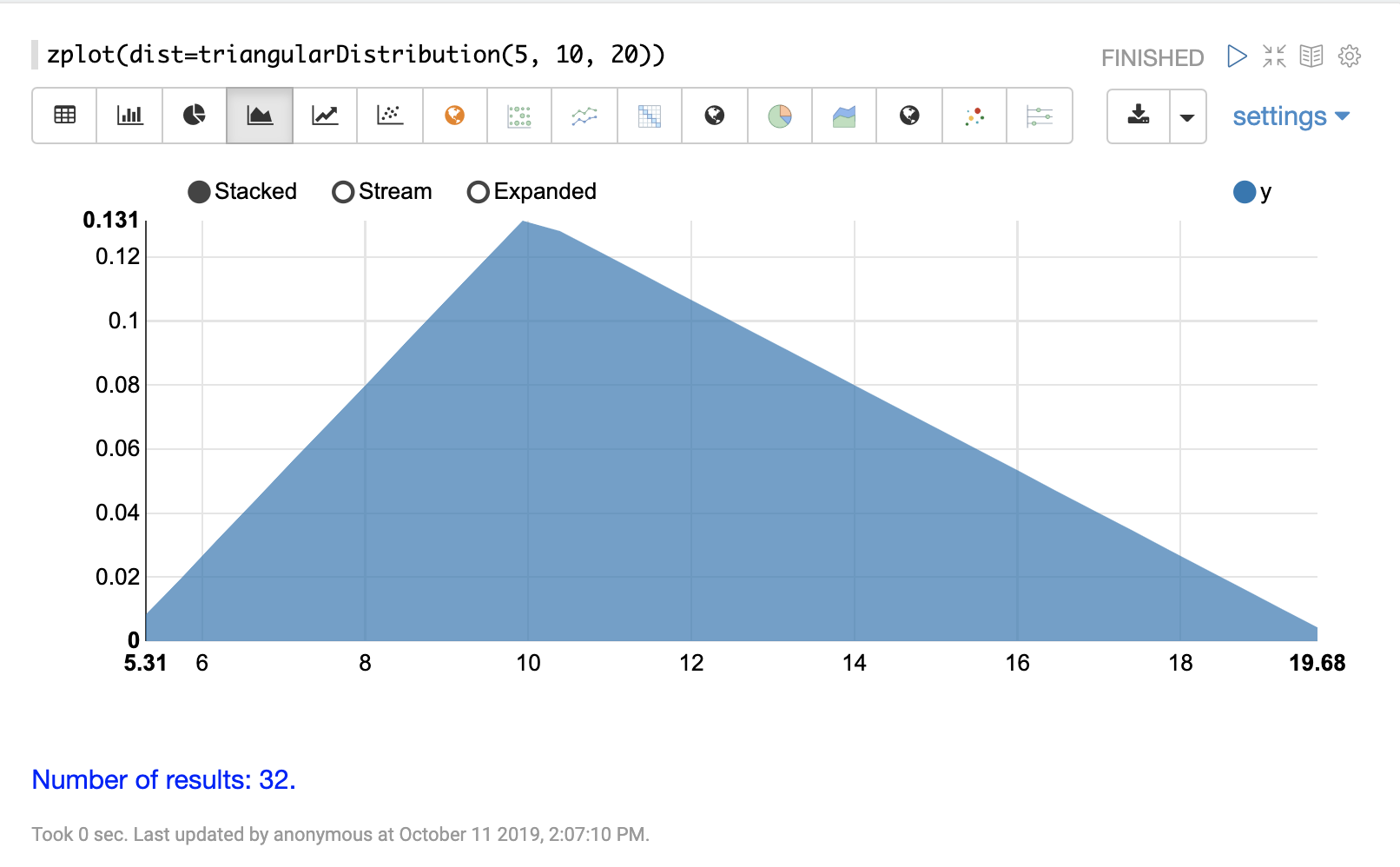
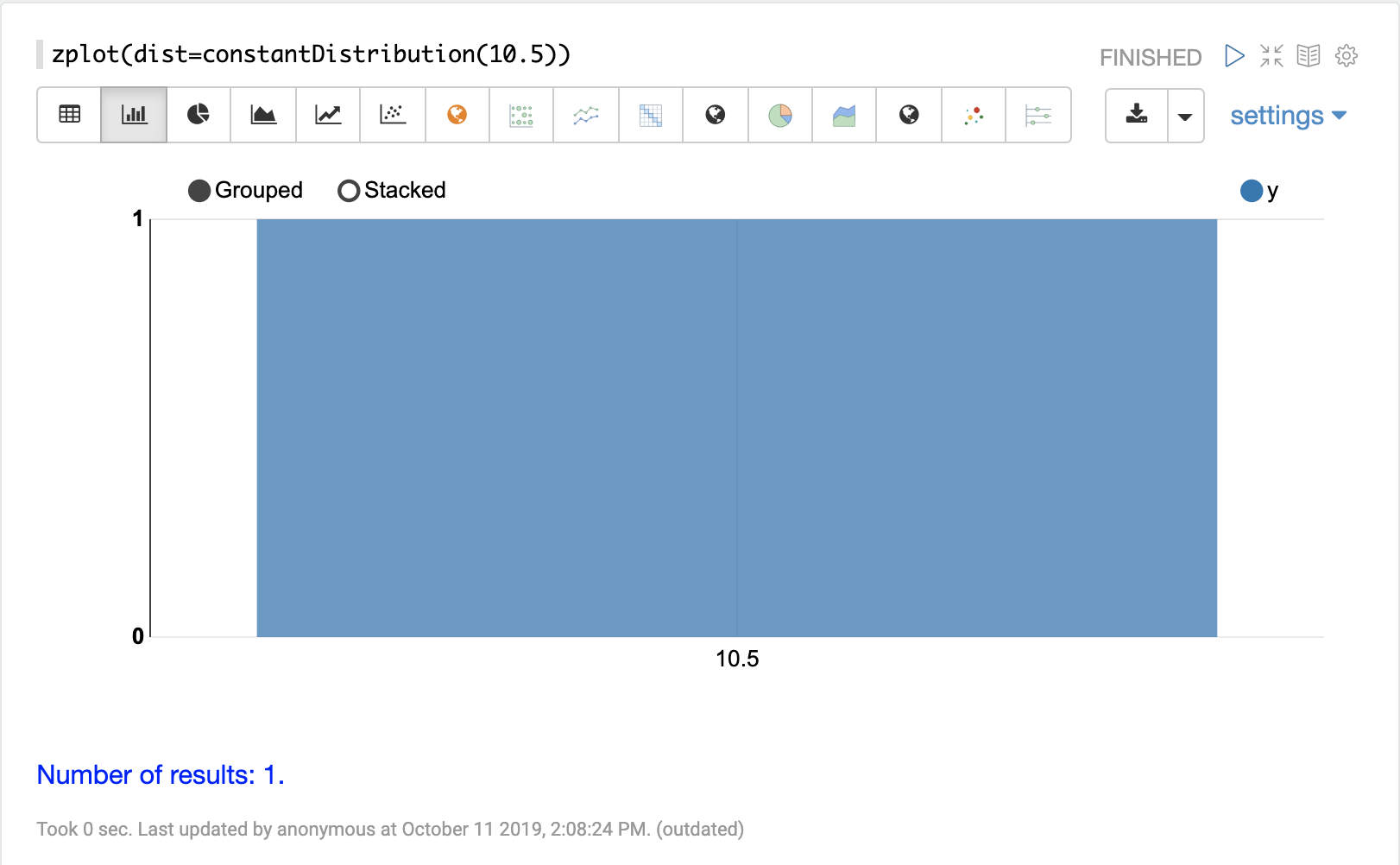
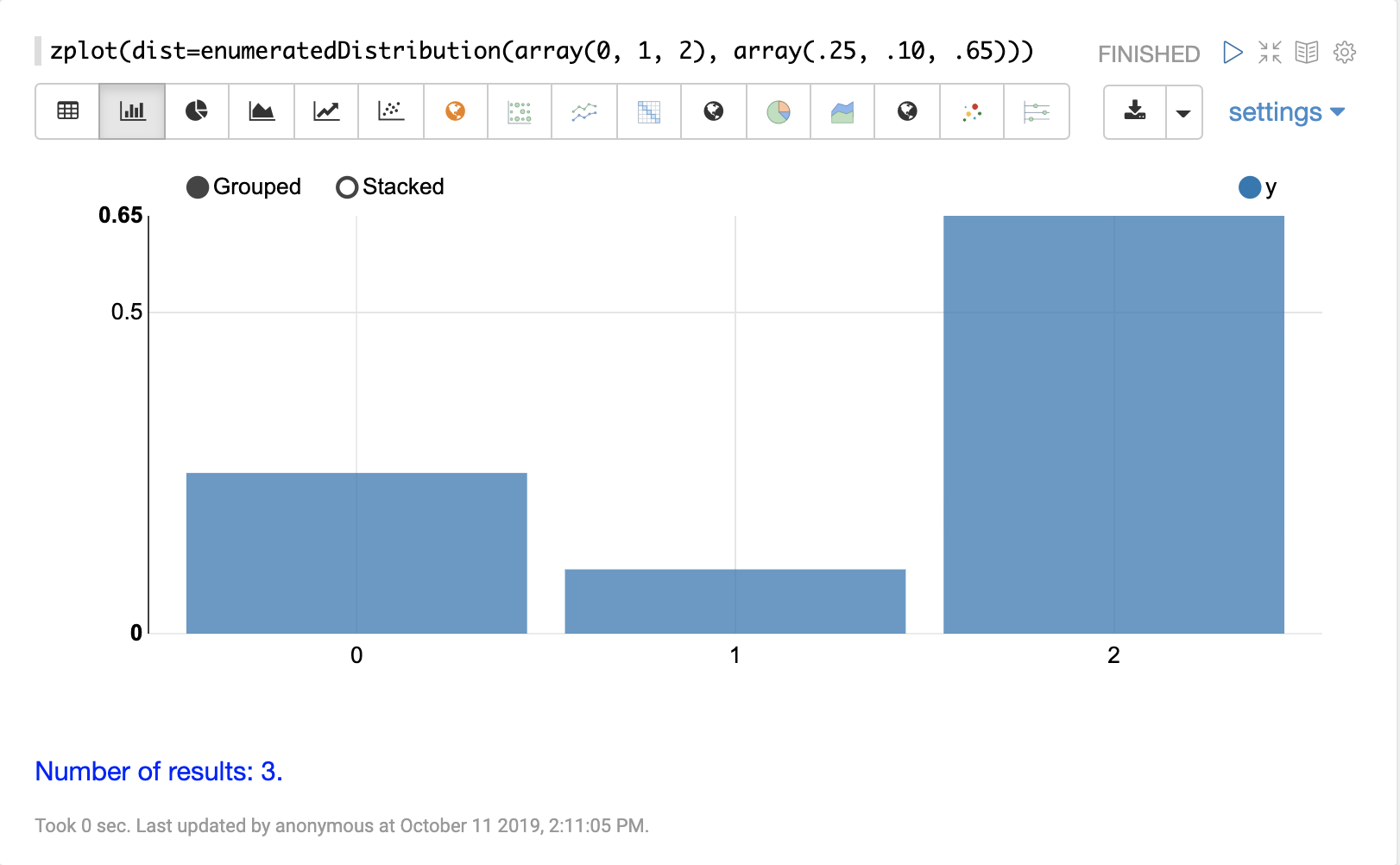
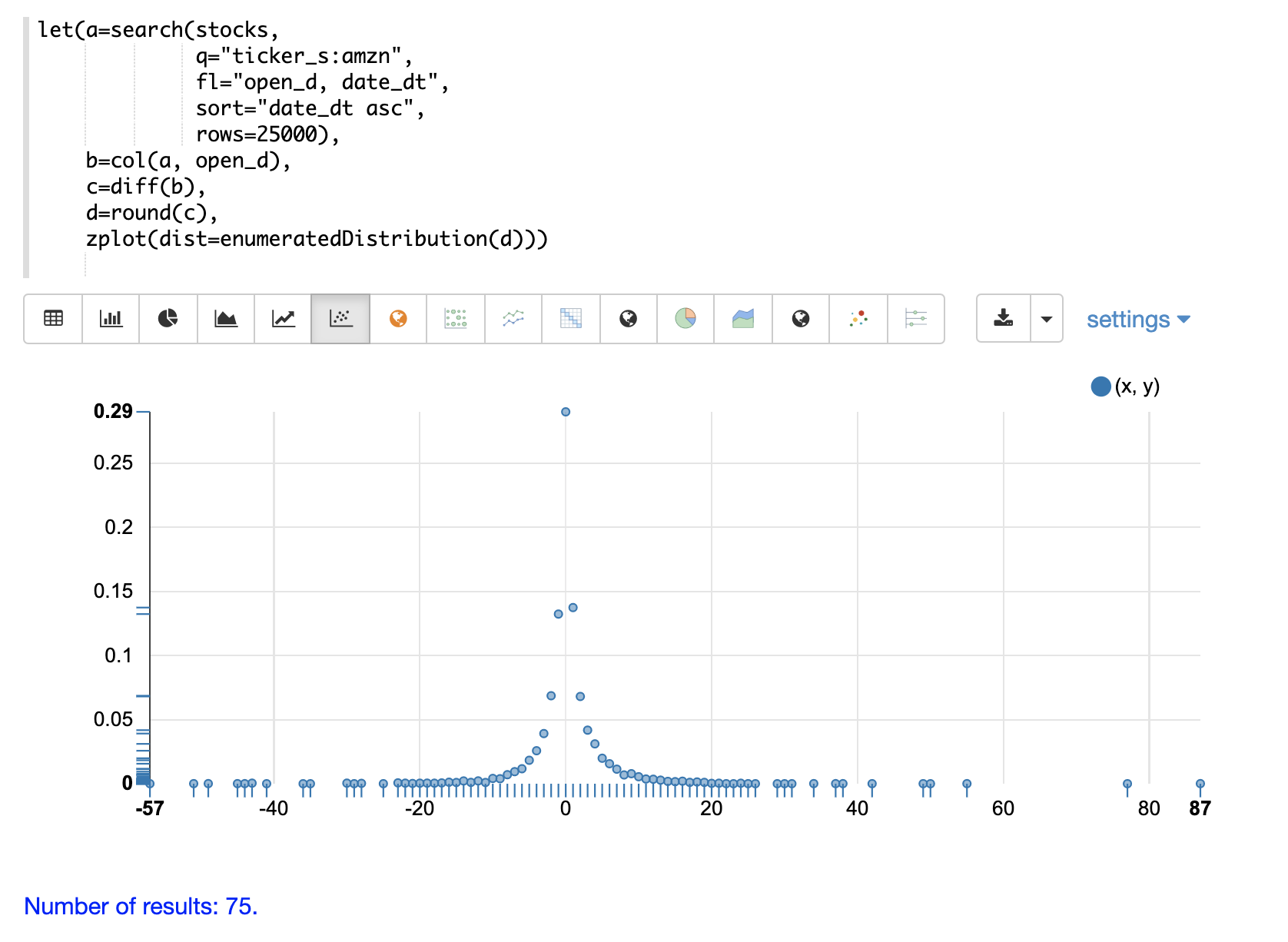
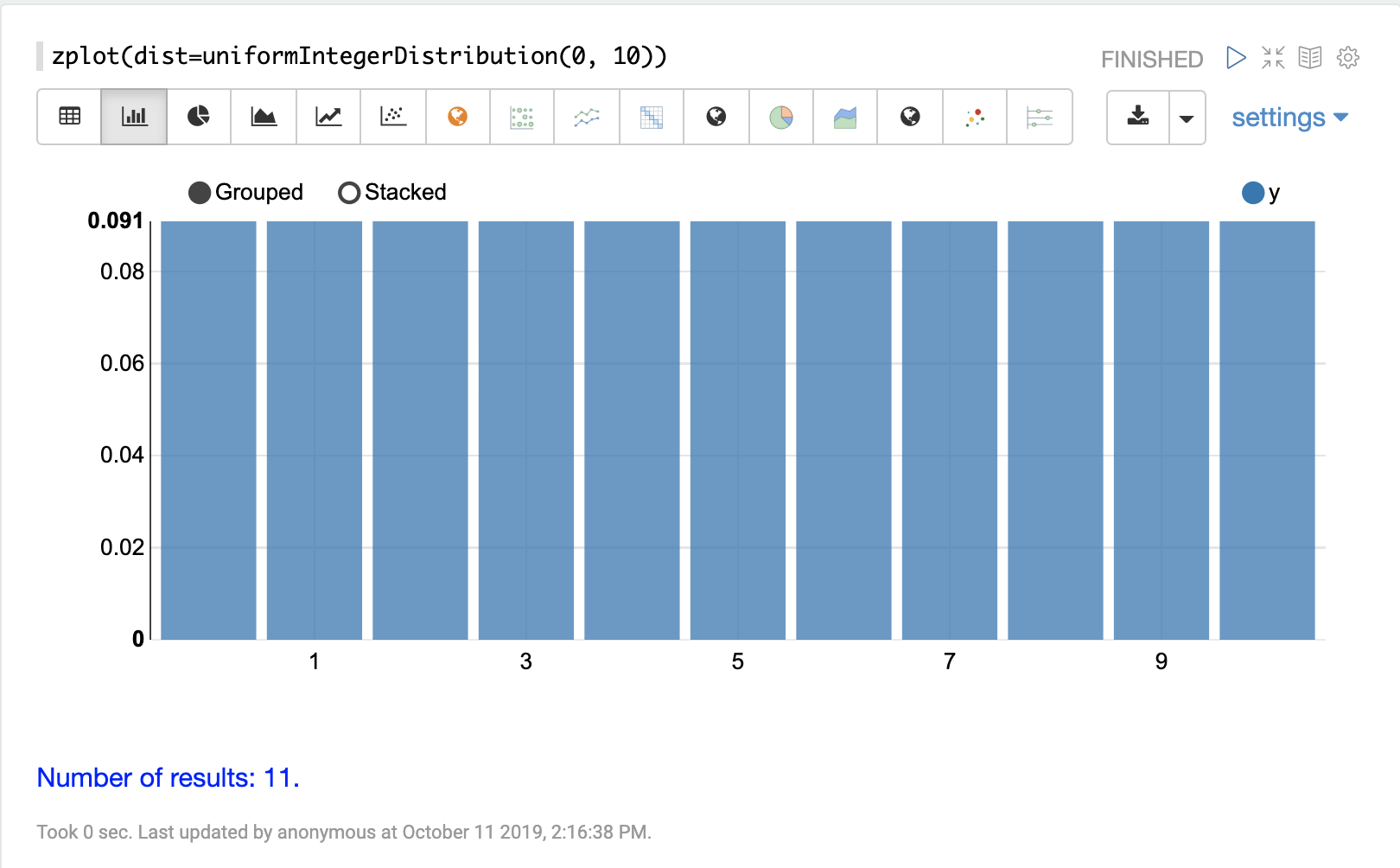
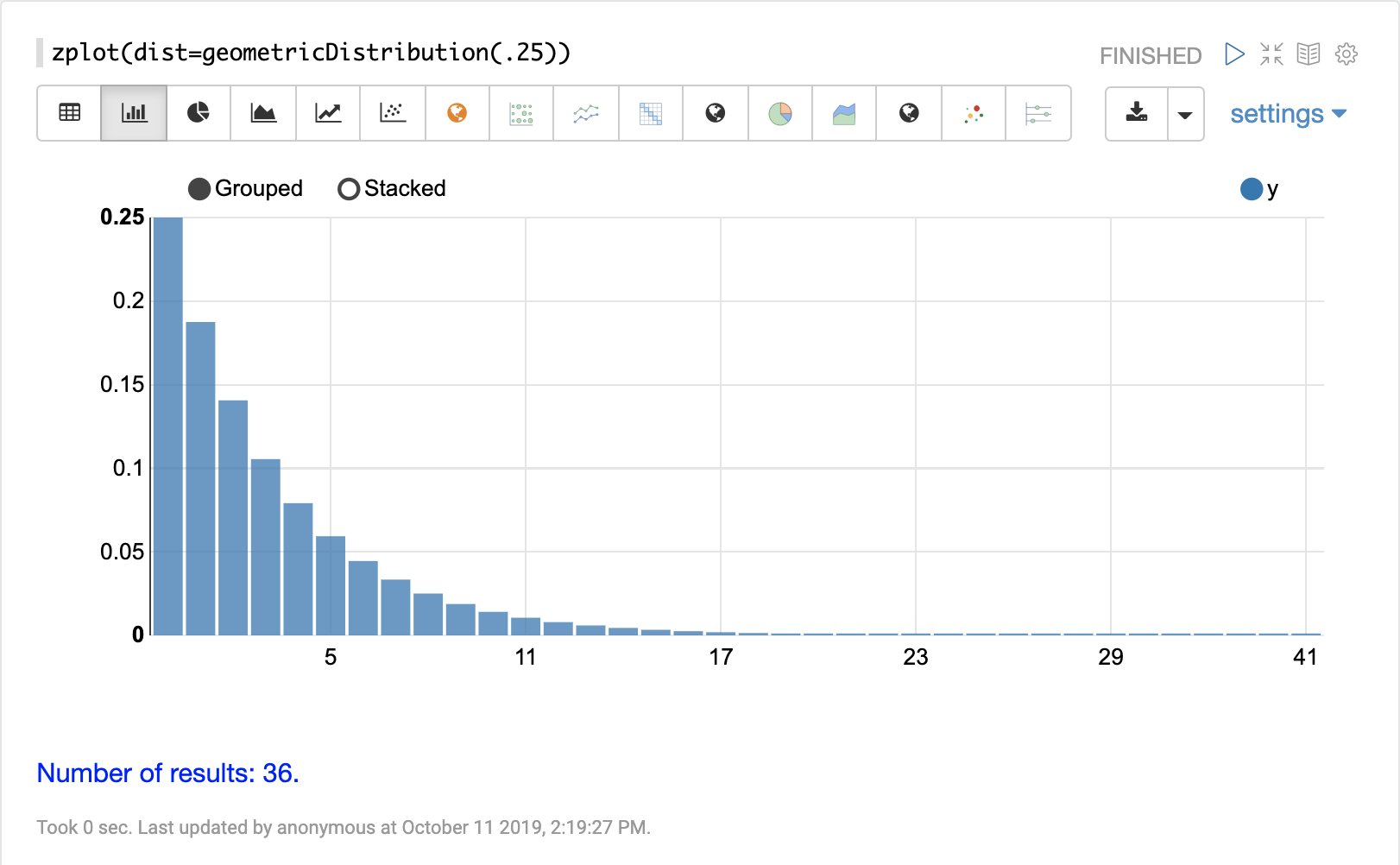
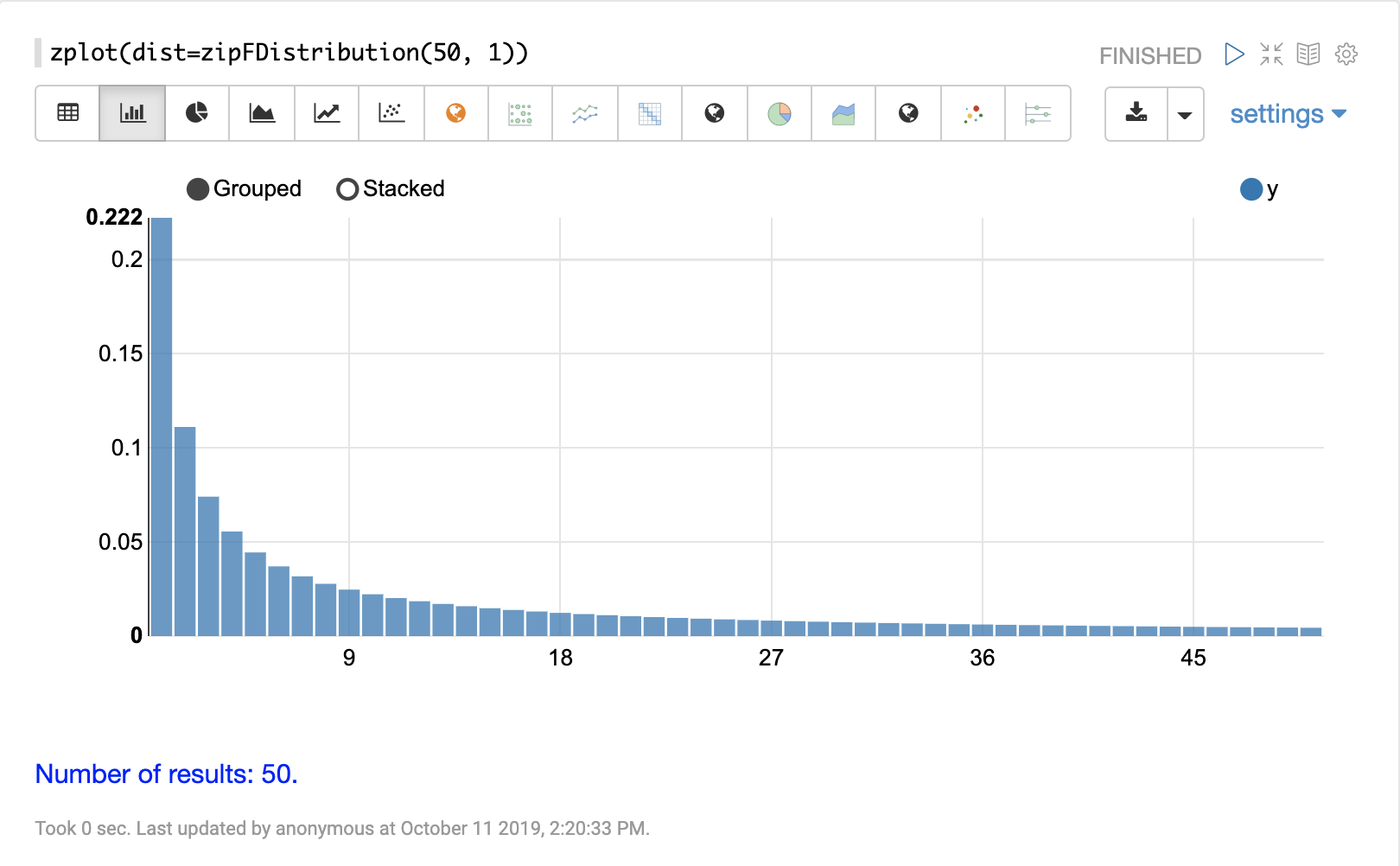
機率分佈可以使用 Zeppelin-Solr，透過具有 dist 參數的 zplot 函數來視覺化，此參數會視覺化分佈的機率密度函數 (PDF)。

以下每個分佈都會顯示範例視覺化。

連續分佈

連續機率分佈適用於連續數字（浮點數）。以下是支援的連續機率分佈。

empiricalDistribution

empiricalDistribution 函數會從實際資料建立連續機率分佈。

經驗分佈可以用於方便地視覺化來自 SolrCloud 集合的隨機樣本的機率密度函數。以下範例顯示 zplot 函數視覺化具有 32 個區間直方圖的隨機樣本的機率密度。

$empirical$

normalDistribution

下方的視覺化顯示平均數為 0 且標準差為 1 的常態分佈。

$dist$

logNormalDistribution

下方的視覺化顯示形狀為 .25 且尺度為 0 的對數常態分佈。

$lognormal$

gammaDistribution

下方的視覺化顯示形狀為 7.5 且尺度為 1 的伽瑪分佈。

$gamma$

betaDistribution

下方的視覺化顯示形狀 1 為 2 且形狀 2 為 2 的貝他分佈。

$beta$

uniformDistribution

下方的視覺化顯示介於 0 和 10 之間的均勻分佈。

$uniformr$

weibullDistribution

下方的視覺化顯示形狀為 5 且尺度為 1 的韋伯分佈。

$weibull$

triangularDistribution

下方的視覺化顯示低值為 5、眾數為 10 且高值為 20 的三角分佈。

$triangular$

constantDistribution

下方的視覺化顯示常數分佈 10.5。

$constant$

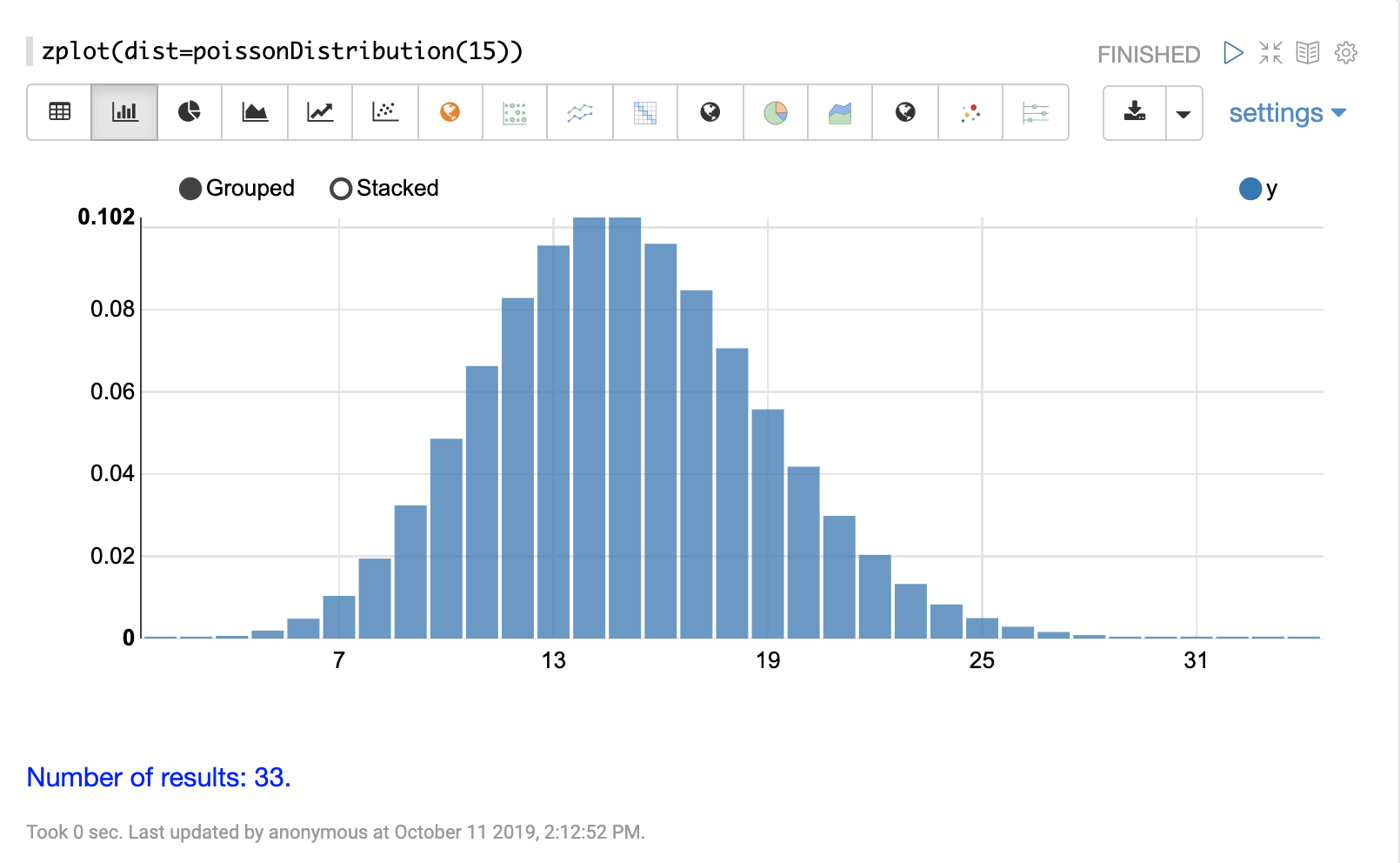
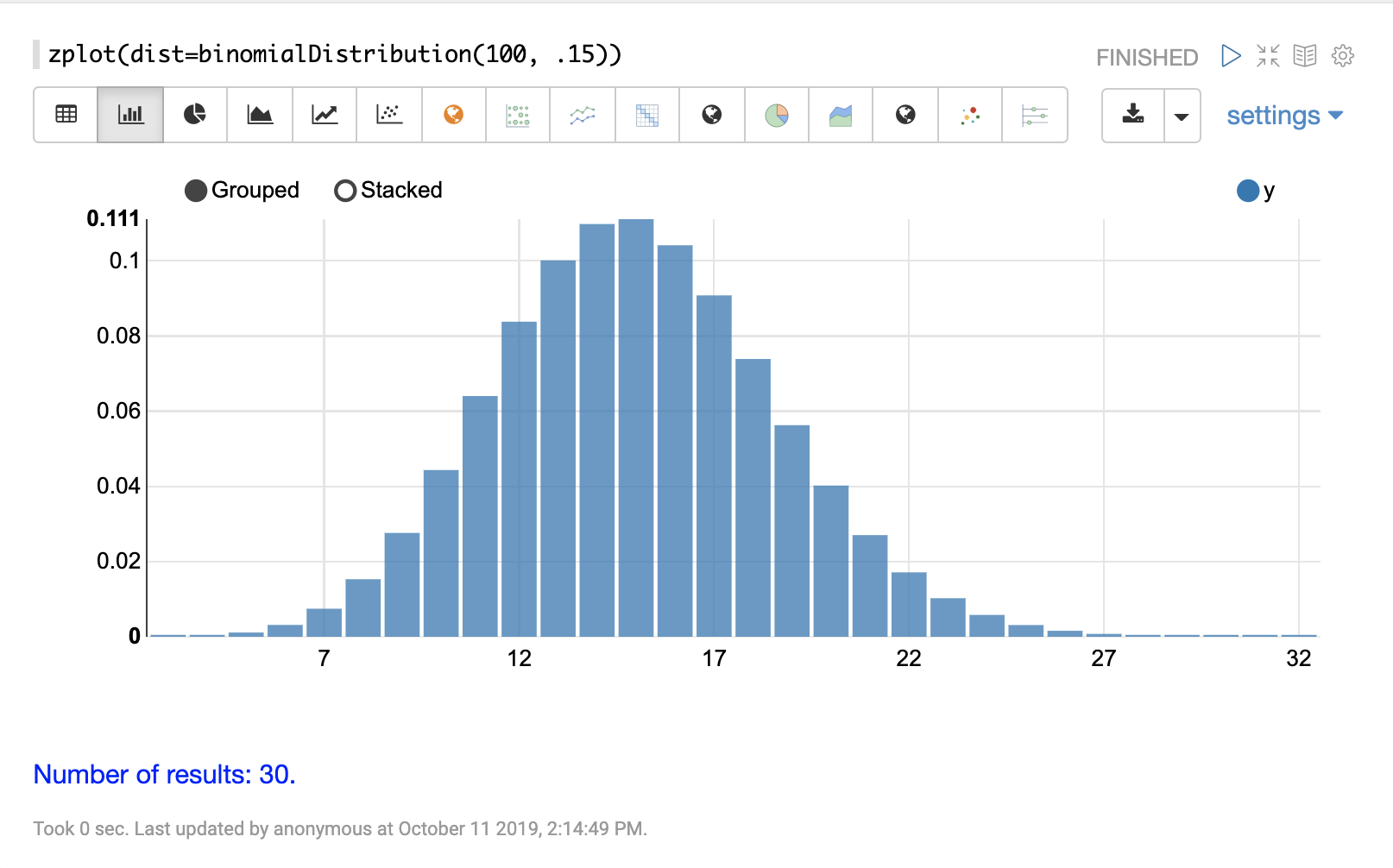
離散分佈

離散機率分佈適用於離散數字（整數）。以下是支援的離散機率分佈。

enumeratedDistribution

enumeratedDistribution 函數會從列舉值和機率清單或從離散值資料集建立離散分佈函數。

下方的視覺化顯示從離散值和機率清單建立的列舉分佈。

$enum1$

下方的視覺化顯示從已轉換為離散值向量的搜尋結果產生的列舉分佈。

$enum2$

poissonDistribution

下方的視覺化顯示平均數為 15 的波松分佈。

$poisson$

binomialDistribution

下方的視覺化顯示具有 100 次試驗和 .15 成功機率的二項分佈。

$binomial$

uniformIntegerDistribution

下方的視覺化顯示介於 0 和 10 之間的均勻整數分佈。

$uniform$

geometricDistribution

下方的視覺化圖表顯示成功機率為 0.25 的幾何分佈機率。

$geometric$

zipF 分佈

下方的視覺化圖表顯示大小為 50，指數為 1 的 ZipF 分佈。

$zipf$

累積機率

cumulativeProbability 函式可與所有機率分佈搭配使用，以計算特定分佈中遇到特定隨機變數的累積機率。

以下範例示範如何計算常態分佈中隨機變數的累積機率。

let(a=normalDistribution(10, 5),
    b=cumulativeProbability(a, 12))

在此範例中，建立一個平均值為 10，標準差為 5 的常態分佈函式。然後計算此特定分佈中數值 12 的累積機率。

當此運算式傳送到 /stream 處理器時，它會回應：

{
  "result-set": {
    "docs": [
      {
        "b": 0.6554217416103242
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

機率

所有機率分佈都可以計算值範圍之間的機率。

在以下範例中，從記錄集合中提取的檔案大小樣本建立經驗分佈。然後計算檔案大小在 40000 到 41000 範圍內的機率為 19%。

let(a=random(logs, q="*:*", fl="filesize_d", rows="50000"),
    b=col(a, filesize_d),
    c=empiricalDistribution(b, 100),
    d=probability(c, 40000, 41000))

當此運算式傳送到 /stream 處理器時，它會回應：

{
  "result-set": {
    "docs": [
      {
        "d": 0.19006540560734791
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 550
      }
    ]
  }
}

離散機率

probability 函式可以與任何離散分佈函式搭配使用，以計算離散值的機率。

以下範例計算卜瓦松分佈中離散值的機率。

在此範例中，建立一個平均值為 100 的卜瓦松分佈函式。然後計算此特定分佈中遇到離散值 101 樣本的機率。

let(a=poissonDistribution(100),
    b=probability(a, 101))

當此運算式傳送到 /stream 處理器時，它會回應：

{
  "result-set": {
    "docs": [
      {
        "b": 0.039466333474403106
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

取樣

所有機率分佈都支援取樣。 sample 函式會從機率分佈中傳回一個或多個隨機樣本。

以下範例示範如何從常態分佈中提取單一樣本。

let(a=normalDistribution(10, 5),
    b=sample(a))

當此運算式傳送到 /stream 處理器時，它會回應：

{
  "result-set": {
    "docs": [
      {
        "b": 11.24578055004963
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

sample 函式也可以傳回樣本向量。樣本向量可以視覺化為散佈圖，以直觀地了解基礎分佈。

第一個範例顯示平均值為 0，標準差為 5 的常態分佈散佈圖。

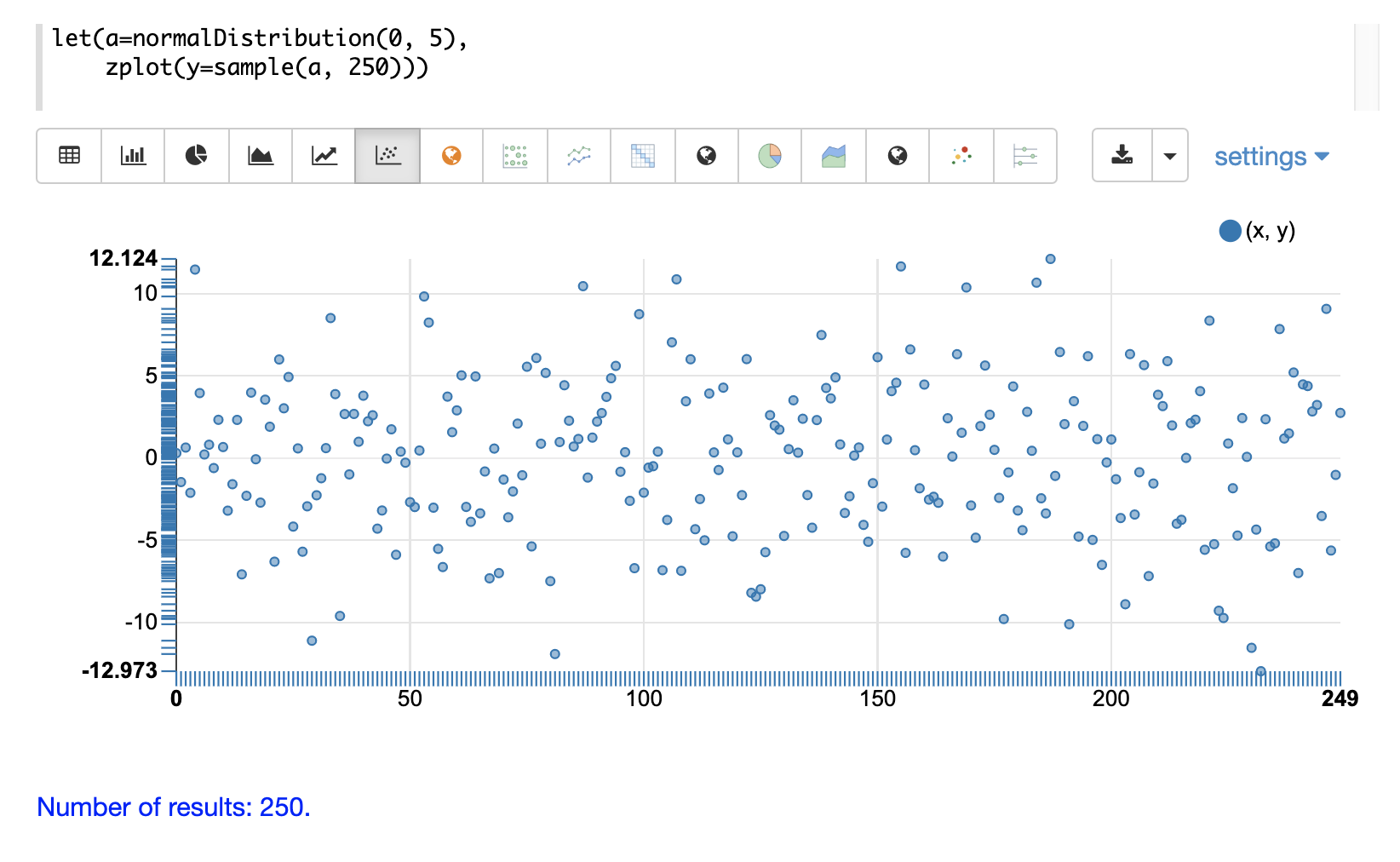
$sample scatter$

下一個範例顯示相同分佈的散佈圖，並對樣本向量套用遞增排序。

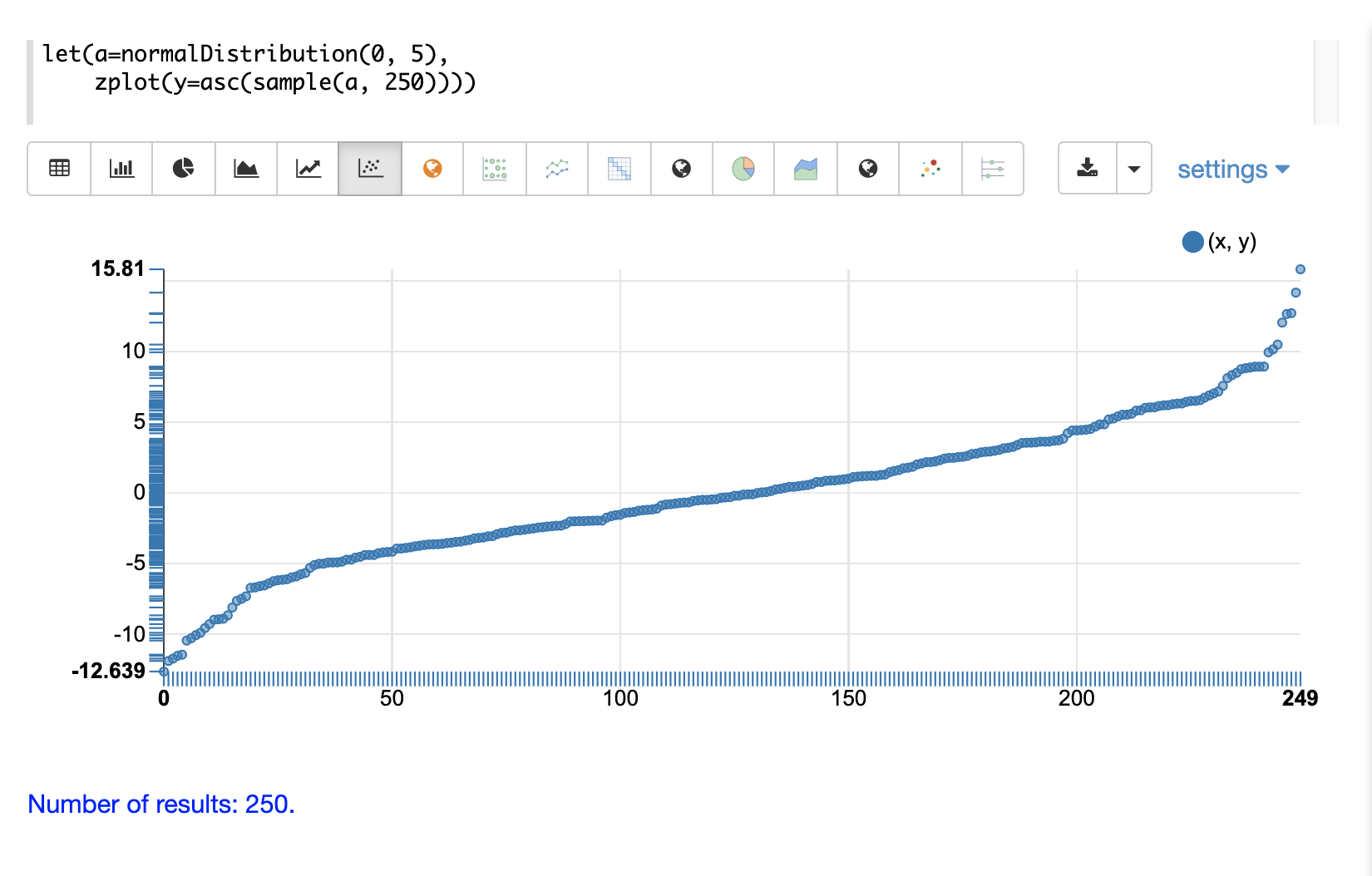
$sample scatter1$

下一個範例顯示在同一個散佈圖中疊加兩個不同的分佈。

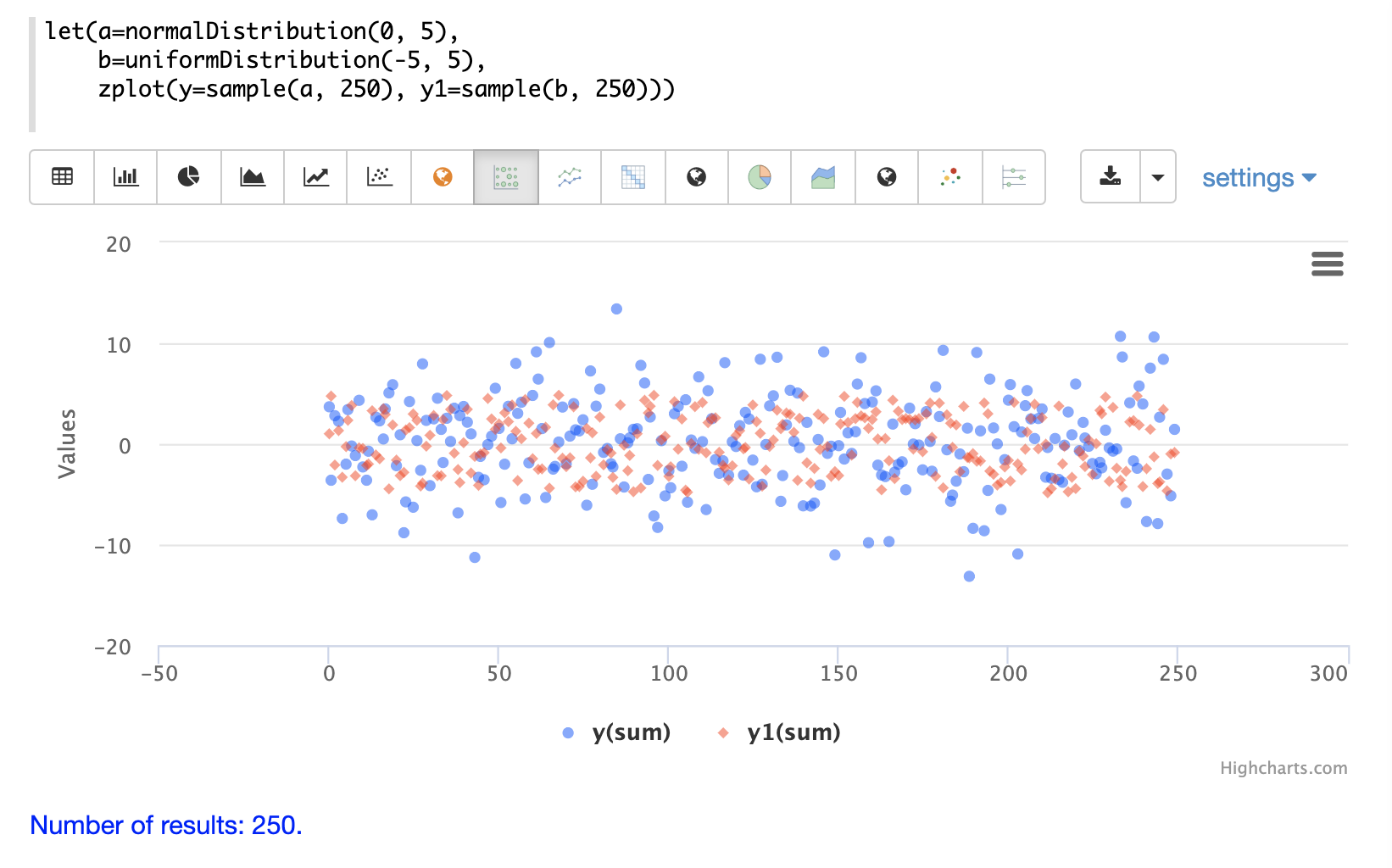
$sample overlay$

多變量常態分佈

多變量常態分佈是將單變量常態分佈推廣到更高維度的概念。

多變量常態分佈對兩個或多個呈常態分佈的隨機變數進行建模。變數之間的關係由共變異數矩陣定義。

取樣

sample 函式可用於從多變量常態分佈中提取樣本，其方式與單變量常態分佈非常相似。

不同之處在於，每個樣本都會是一個陣列，其中包含從每個基礎常態分佈中提取的樣本。如果提取多個樣本，sample 函式會傳回一個矩陣，每列包含一個樣本。從長遠來看，樣本矩陣的各列會符合用於參數化多變量常態分佈的共變異數矩陣。

以下範例示範如何初始化多變量常態分佈並從中提取樣本。

在此範例中，從記錄集合中選取 5000 個隨機樣本。每個樣本都包含欄位 filesize_d 和 response_d。這兩個欄位的值都符合常態分佈。

然後將這兩個欄位向量化。filesize_d 向量儲存在變數 b 中，而 response_d 變數儲存在變數 c 中。

建立一個陣列，其中包含兩個向量化欄位的平均值。

然後將兩個向量加入一個轉置的矩陣。這會建立一個觀察矩陣，其中每列包含一個 filesize_d 和 response_d 的觀察值。然後使用 cov 函式從觀察矩陣的各列建立共變異數矩陣。共變異數矩陣描述 filesize_d 和 response_d 之間的共變異數。

然後使用兩個欄位的平均值陣列和共變異數矩陣呼叫 multivariateNormalDistribution 函式。多變量常態分佈的模型會指定給變數 g。

最後，從多變量常態分佈中提取五個樣本。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, response_d"),
    b=col(a, filesize_d),
    c=col(a, response_d),
    d=array(mean(b), mean(c)),
    e=transpose(matrix(b, c)),
    f=cov(e),
    g=multiVariateNormalDistribution(d, f),
    h=sample(g, 5))

這些樣本會以矩陣形式傳回，其中每列代表一個樣本。矩陣中有兩列。第一列包含 filesize_d 的樣本，第二列包含 response_d 的樣本。從長遠來看，各列之間的共變異數會符合用於實例化多變量常態分佈的共變異數矩陣。

{
  "result-set": {
    "docs": [
      {
        "h": [
          [
            41974.85669321393,
            779.4097049705296
          ],
          [
            42869.19876441414,
            834.2599296790783
          ],
          [
            38556.30444839889,
            720.3683470060988
          ],
          [
            37689.31290928216,
            686.5549428100018
          ],
          [
            40564.74398214547,
            769.9328090774
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 162
      }
    ]
  }
}