數位訊號處理
使用者指南的這一節探討數位訊號處理 (DSP) 領域中常用的函式。
卷積
conv 函式計算兩個向量的卷積。卷積的計算方式是將第二個向量反轉,並將其滑過第一個向量。當第二個向量滑過第一個向量時,會計算每個點的兩個向量的點積。點積會收集在第三個向量中,這就是兩個向量的卷積。
移動平均函式
在檢視卷積的範例之前,先回顧一下 movingAvg 函式會很有幫助。移動平均函式藉由將視窗滑過向量,並計算每個偏移處的視窗平均值來計算移動平均。如果這聽起來與卷積相似,那是因為 movingAvg 函式涉及與卷積類似的滑動視窗方法。
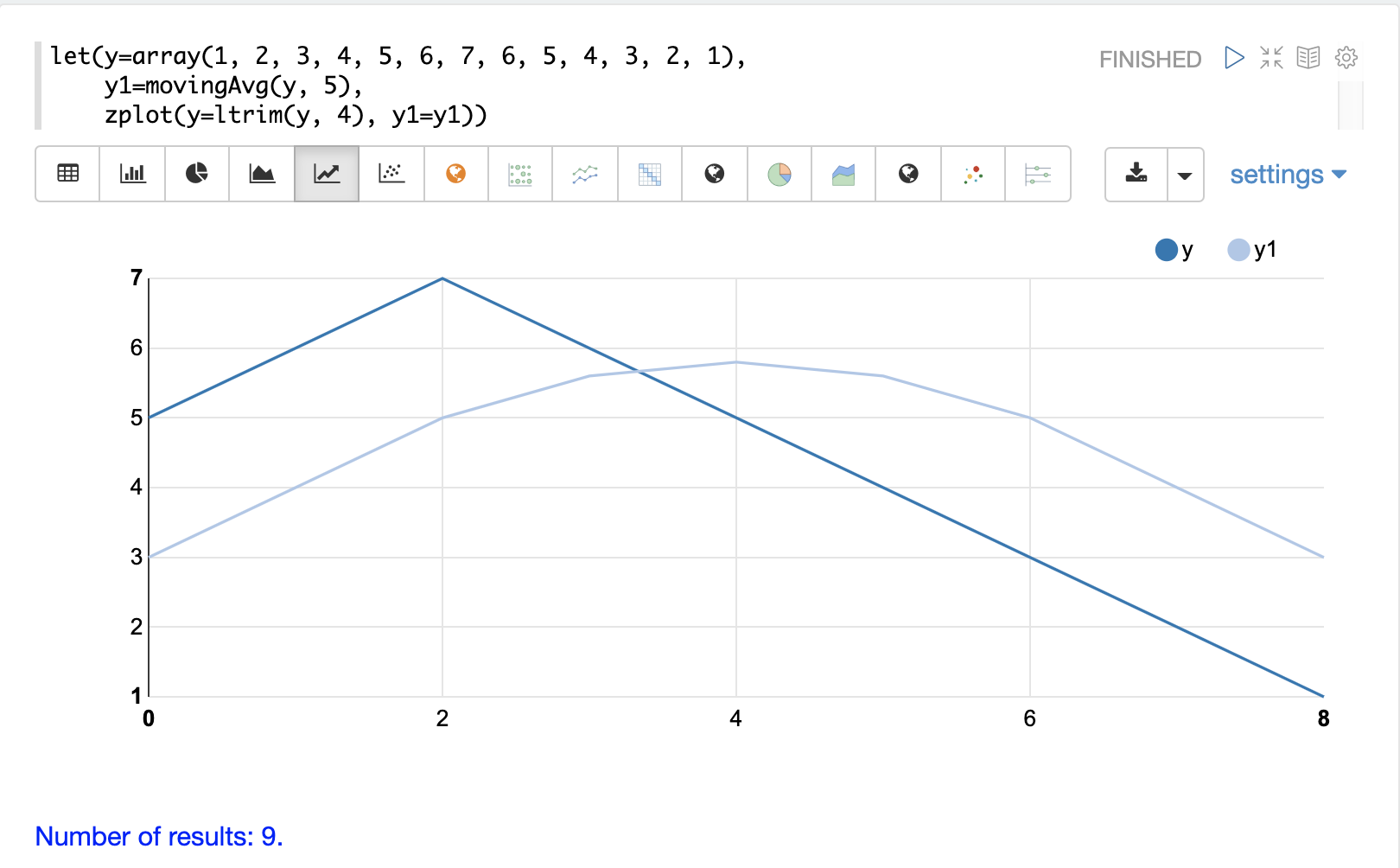
以下是一個視窗大小為 5 的移動平均範例。請注意,原始向量有 13 個元素,但移動平均的結果只有 9 個元素。這是因為 movingAvg 函式只會在有完整視窗時才開始產生結果。ltrim 函式用於從原始 y 陣列修剪前四個元素,以與移動平均對齊。
卷積平滑
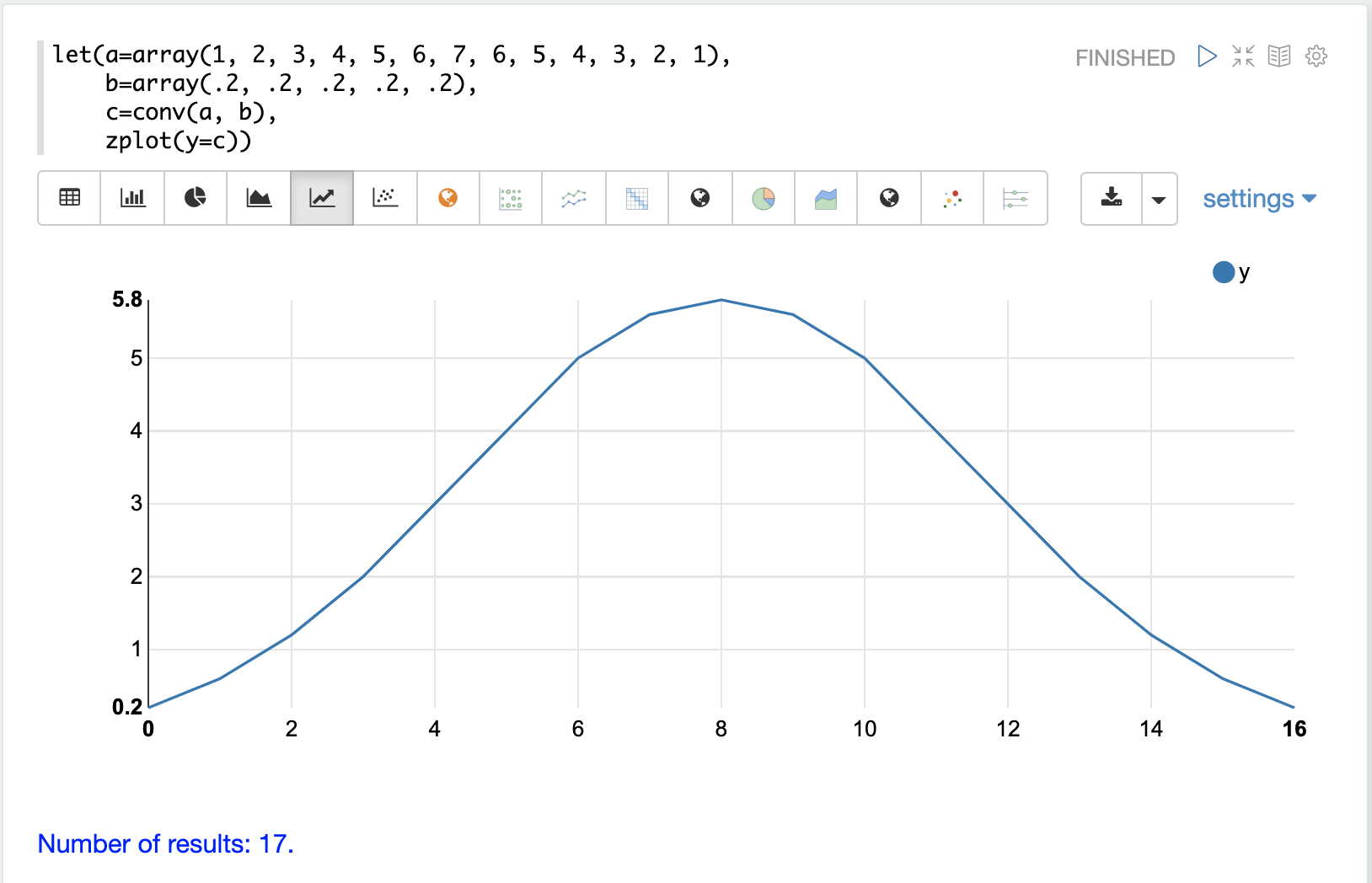
移動平均也可以使用卷積計算。在以下範例中,conv 函式用於計算第一個陣列的移動平均,方法是將第二個陣列作為篩選器套用。
查看結果,我們發現卷積產生了一個具有 17 個值的陣列,而不是移動平均產生的 9 個值。這是因為 conv 函式會在第一個向量的前面和後面填補零,以便視窗大小始終為完整大小。
我們使用 ltrim 和 rtrim 函式修剪卷積結果的前 4 個和最後 4 個值,即可達到與 movingAvg 函式相同的結果。
以下範例在同一個圖表上繪製了修剪後的卷積和移動平均線。請注意,它們完美重疊。
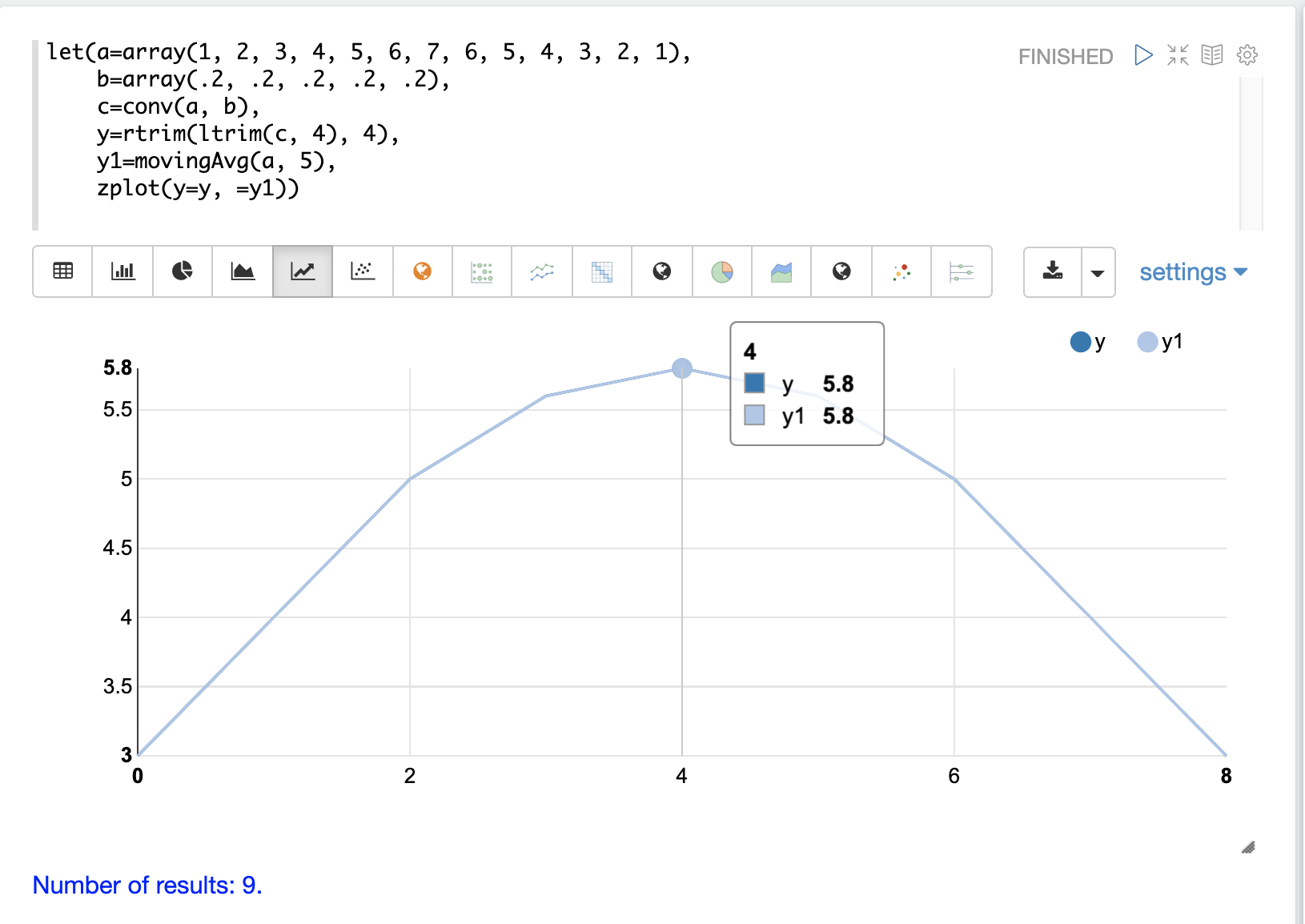
這說明了如何使用卷積來平滑訊號,方法是將濾波器滑過訊號,並在每個點計算點積。平滑效果是由濾波器的設計所造成的。在此範例中,濾波器的長度為 5,且濾波器中的每個值都是 .2。此濾波器計算視窗大小為 5 的簡單移動平均。
使用卷積計算簡單移動平均的公式是使濾波器長度等於視窗大小,並使濾波器的值都相同且總和為 1。可以透過將濾波器變更為長度為 4,且每個值為 .25 來計算視窗大小為 4 的移動平均。
變更權重
濾波器(有時稱為核心)可以被視為權重的向量。在最初的範例中,濾波器中的所有值都具有相同的權重 (.2)。可以變更濾波器中的權重以產生不同的平滑效果。以下範例展示了這一點。
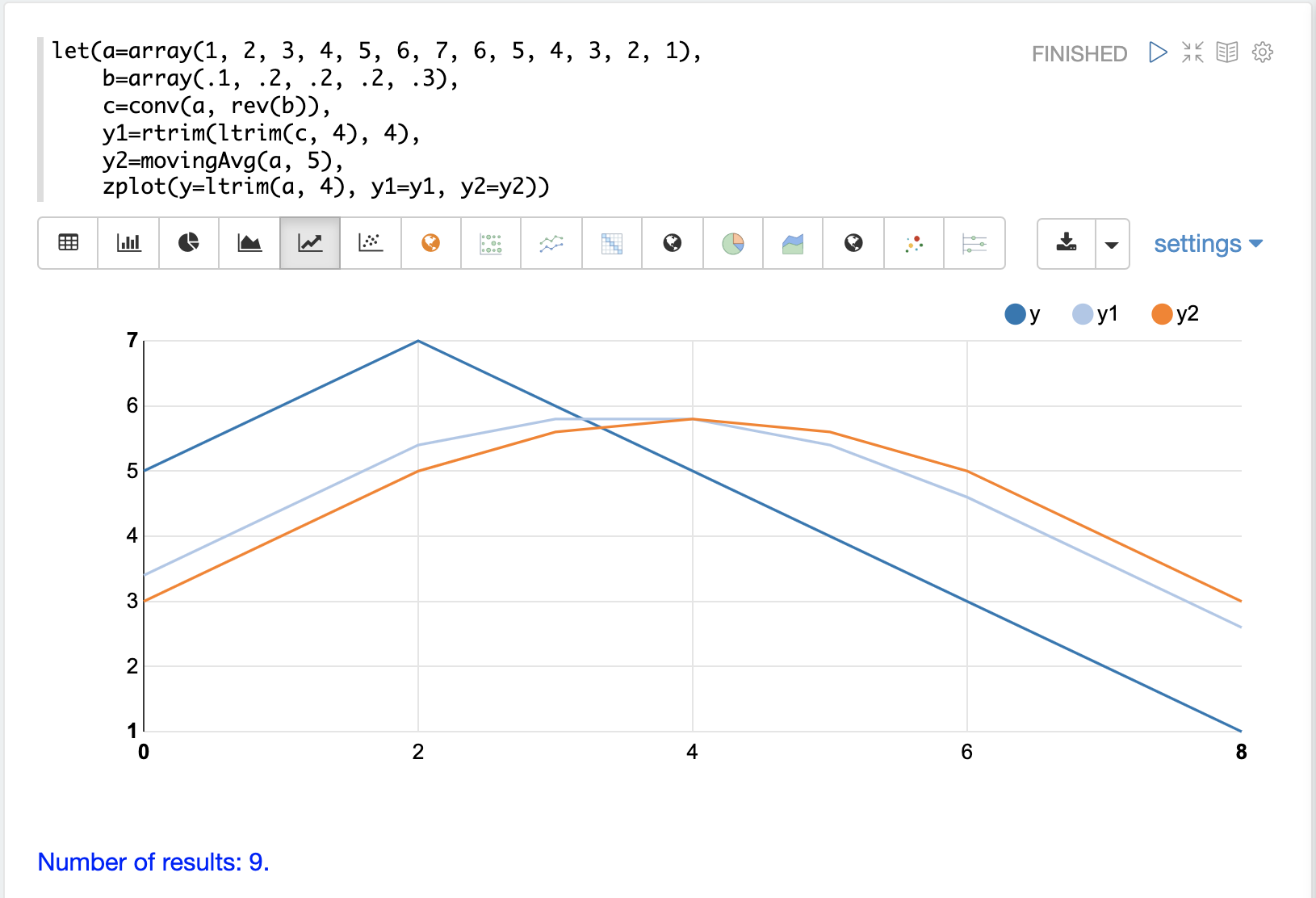
在此範例中,濾波器的權重從 .1 增加到 .3。這會將更多權重放在濾波器的前端。請注意,在 conv 函數應用之前,會使用 rev 函數將濾波器反轉。這樣做的原因是卷積會反轉濾波器。在這種情況下,我們會提前反轉它,當卷積將其反轉回來時,它與原始濾波器相同。
該圖顯示了濾波器中不同權重的效果。深藍色線是初始陣列。淺藍色線是卷積,橙色線是移動平均。請注意,卷積對基礎陣列中的移動反應更快。這是因為更多權重放在濾波器的前端。
互相關
互相關用於確定兩個訊號之間的延遲。這是透過將一個訊號滑過另一個訊號,並在每個位移處計算點積來完成的。點積會被收集到一個向量中,該向量代表每個位移處的相關性。互相關向量中最高的點積是兩個訊號最密切相關的點。
卷積中使用的滑動點積也可以用來表示兩個向量之間的互相關。表示相關性時,公式中唯一的區別是第二個向量不反轉。
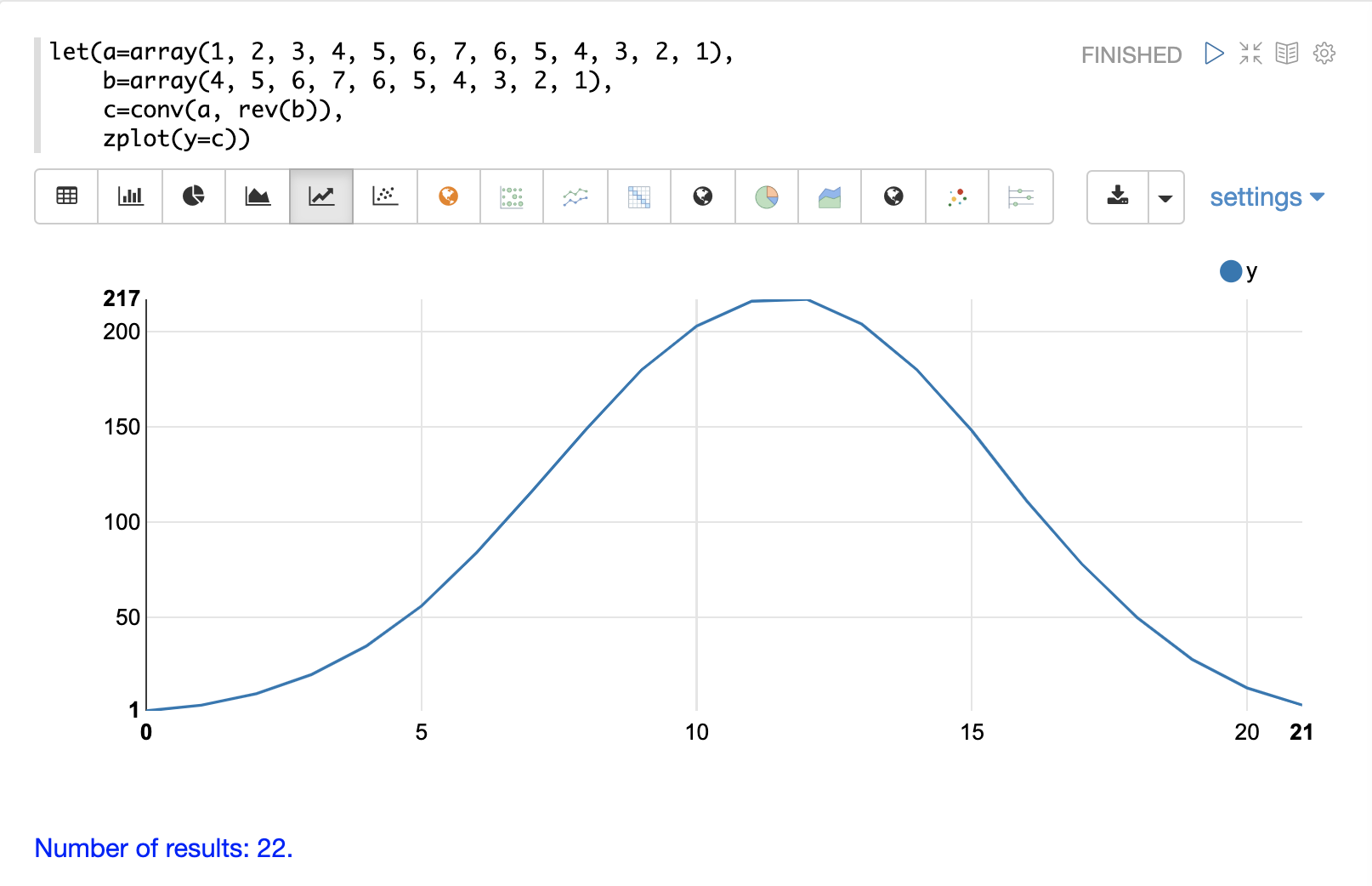
請注意,在以下範例中,第二個向量會先由 rev 函數反轉,然後再由 conv 函數進行運算。conv 函數會反轉第二個向量,因此它會翻轉回原始順序以執行相關性計算,而不是卷積計算。
請注意,結果中的最高值為 217。這是兩個向量具有最高相關性的點。
尋找延遲
從互相關結果計算延遲相當簡單,但可以使用稱為 finddelay 的方便函數來直接尋找延遲。在底層,finddelay 使用卷積數學來計算互相關向量,然後計算兩個訊號之間的延遲。
以下是 finddelay 函數的範例。請注意,finddelay 函數會報告第一個訊號和第二個訊號之間有 3 個週期的延遲。

自相關
自相關會測量訊號與自身相關的程度。自相關用於確定向量是否包含訊號或是否純粹是隨機的。
幾個範例(附帶圖表)將有助於理解這些概念。
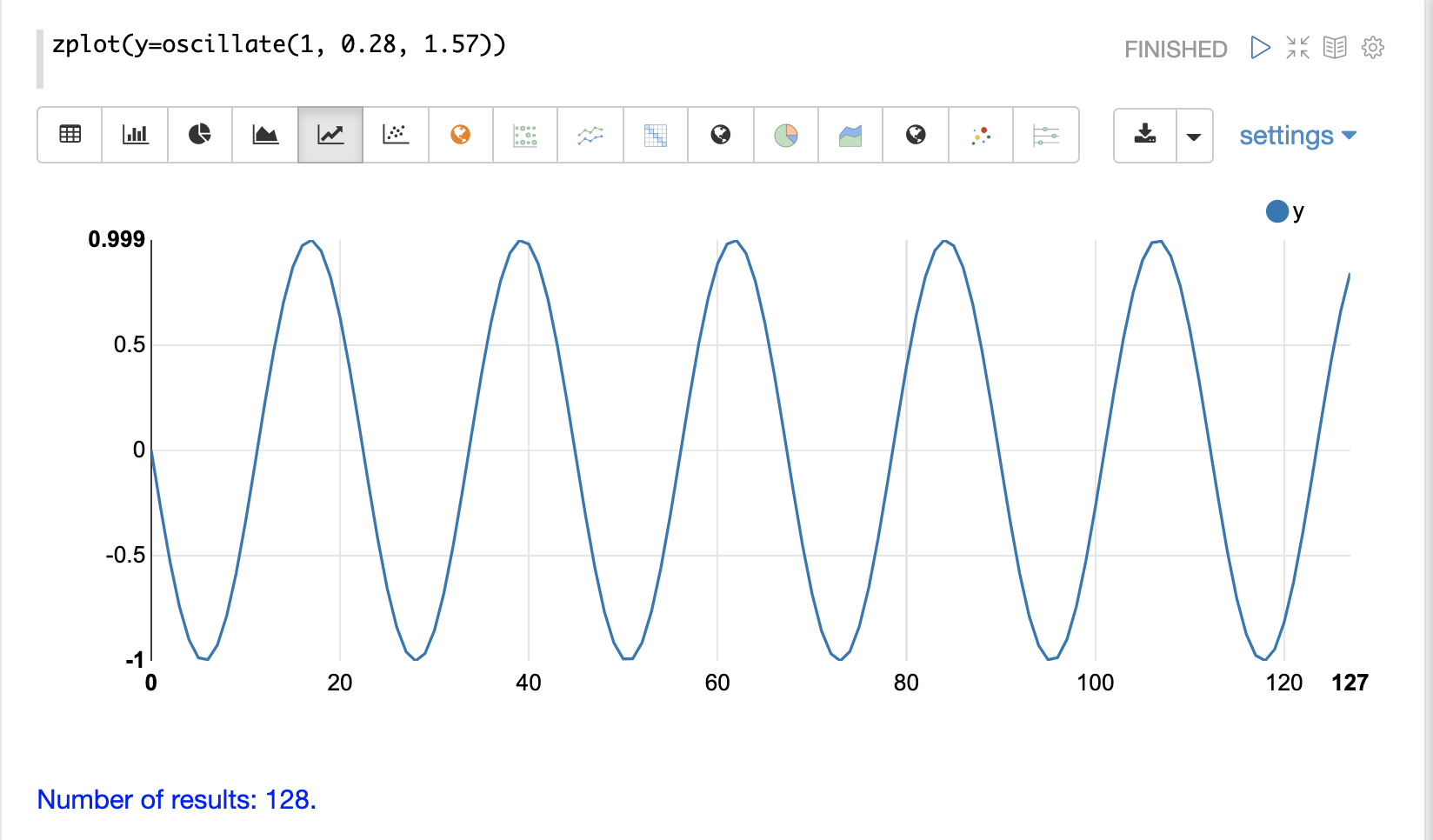
第一個範例只是重新探討上述外插正弦波的範例。其結果繪製在下圖中。請注意,圖表具有明顯非隨機的結構。
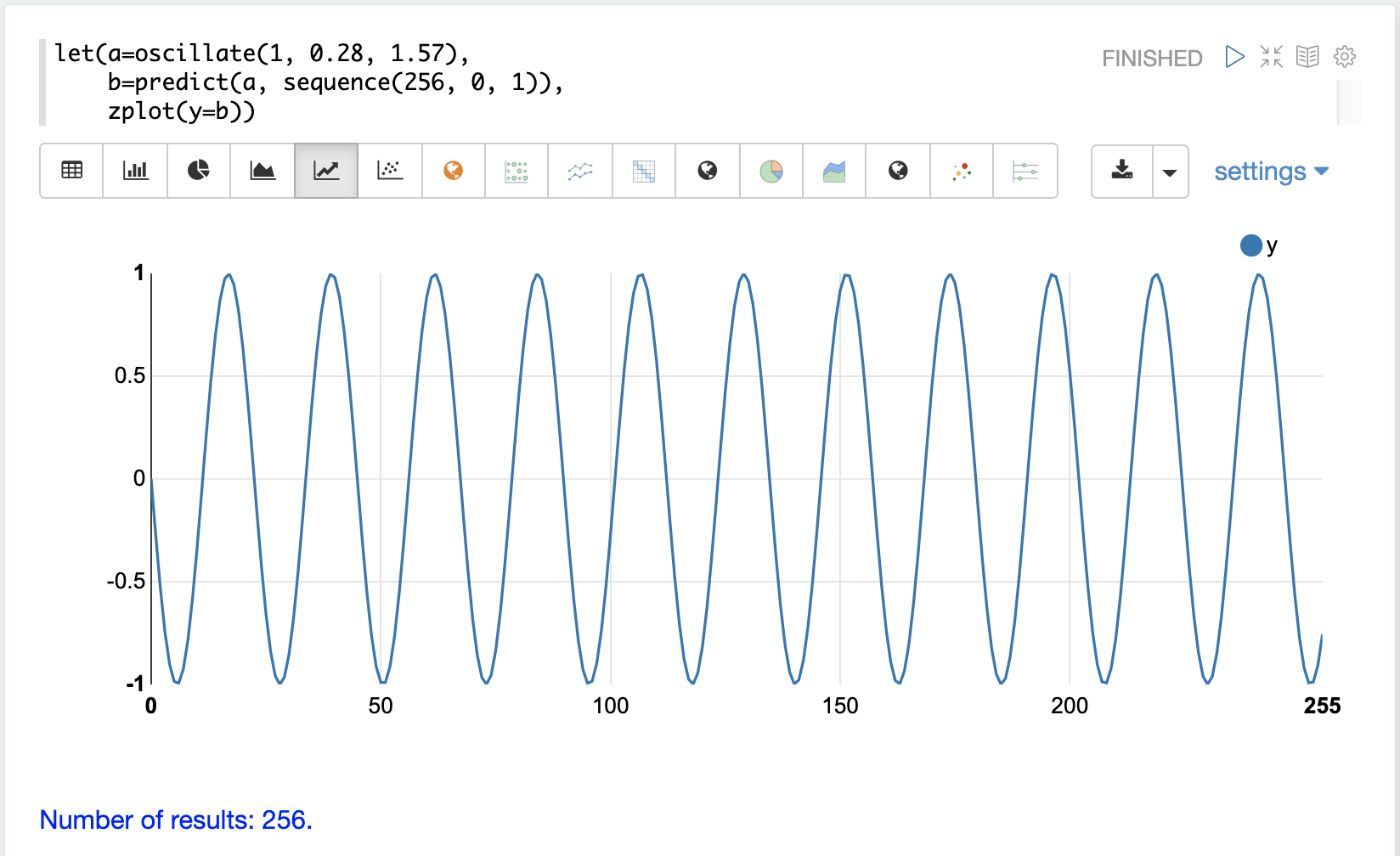
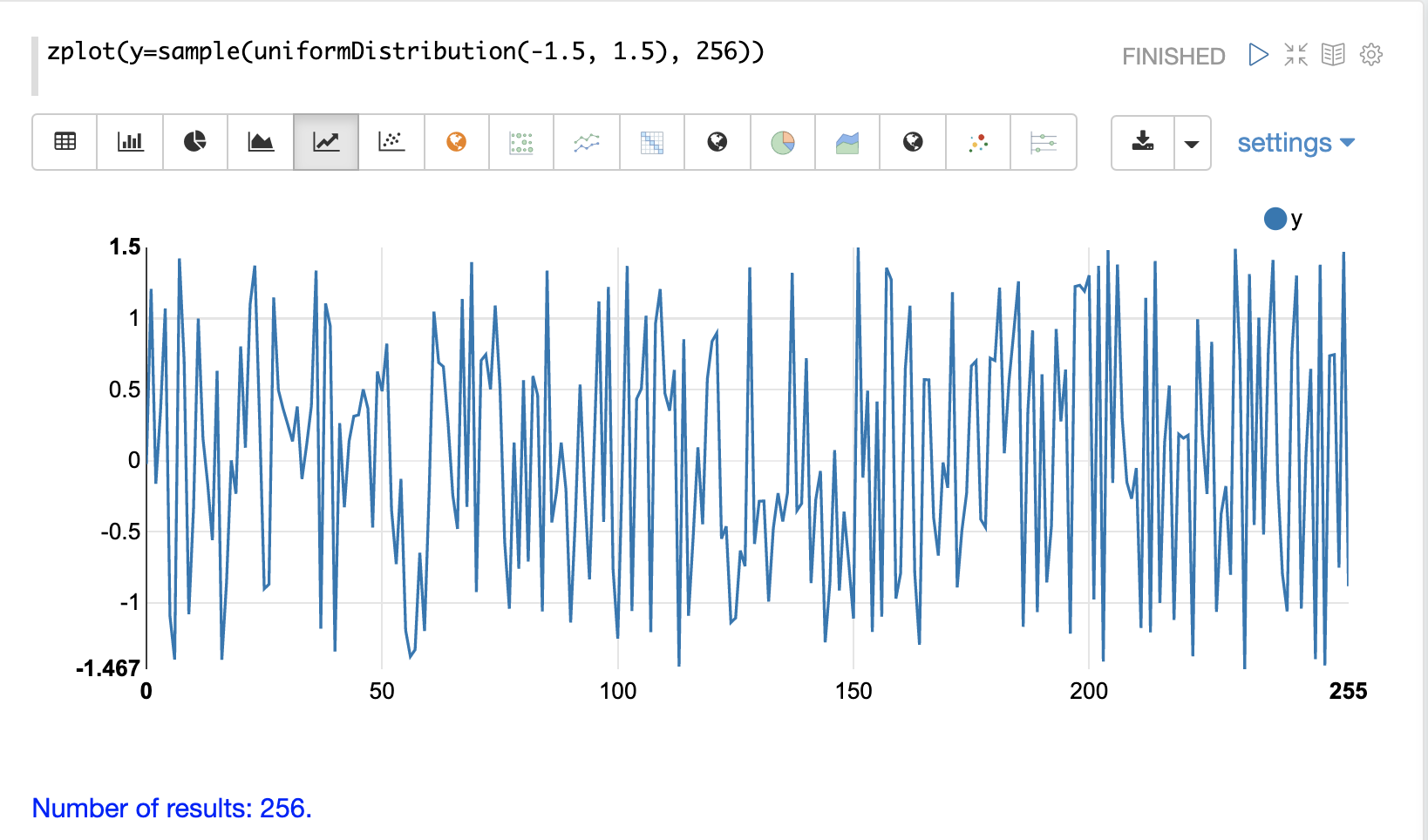
在下一個範例中,sample 函數用於從 uniformDistribution 中取出 256 個樣本,以建立隨機資料向量。其結果繪製在下圖中。請注意,資料沒有明顯的結構,而且資料看起來是隨機的。
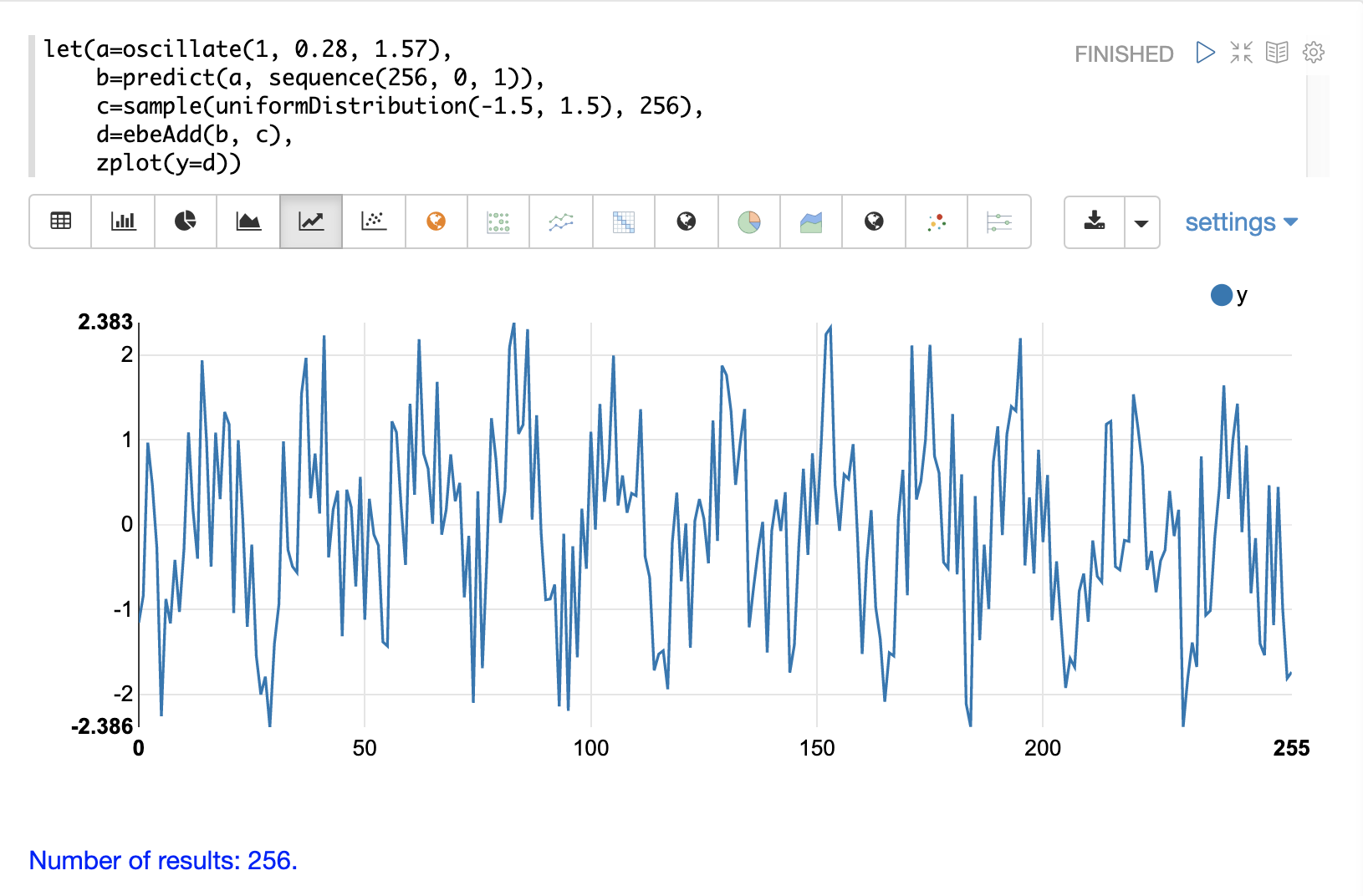
在下一個範例中,會使用 ebeAdd 函數將隨機雜訊加入正弦波。其結果繪製在下圖中。請注意,正弦波在某種程度上被隱藏在雜訊中。很難確定是否有結構。隨著圖表變得更加密集,可能會變得更難以看到隱藏在雜訊中的模式。
在下一個範例中,會使用上面顯示的每個向量執行自相關,以查看自相關圖看起來如何。
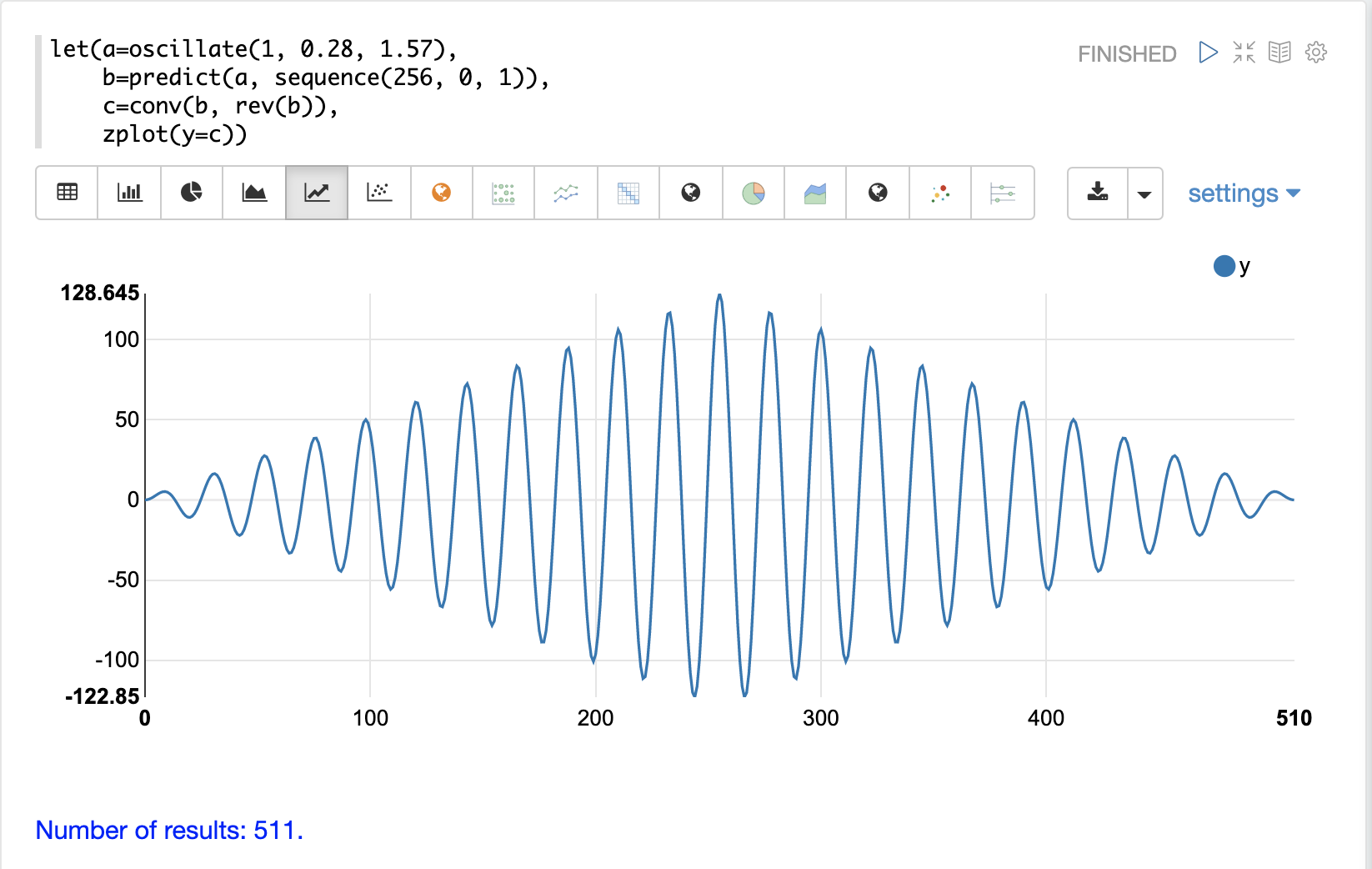
在以下範例中,conv 函數用於自動關聯第一個向量(即正弦波)。請注意,conv 函數只是將正弦波與自身相關聯。
該圖具有非常獨特的結構。當正弦波滑過自身的副本時,相關性會上下移動,強度增加,直到達到峰值。此峰值直接位於中心,是正弦波直接對齊的點。在峰值之後,當正弦波滑動得越來越遠而未直接對齊時,相關性會上下移動,強度會降低。
這是純訊號的自相關圖。
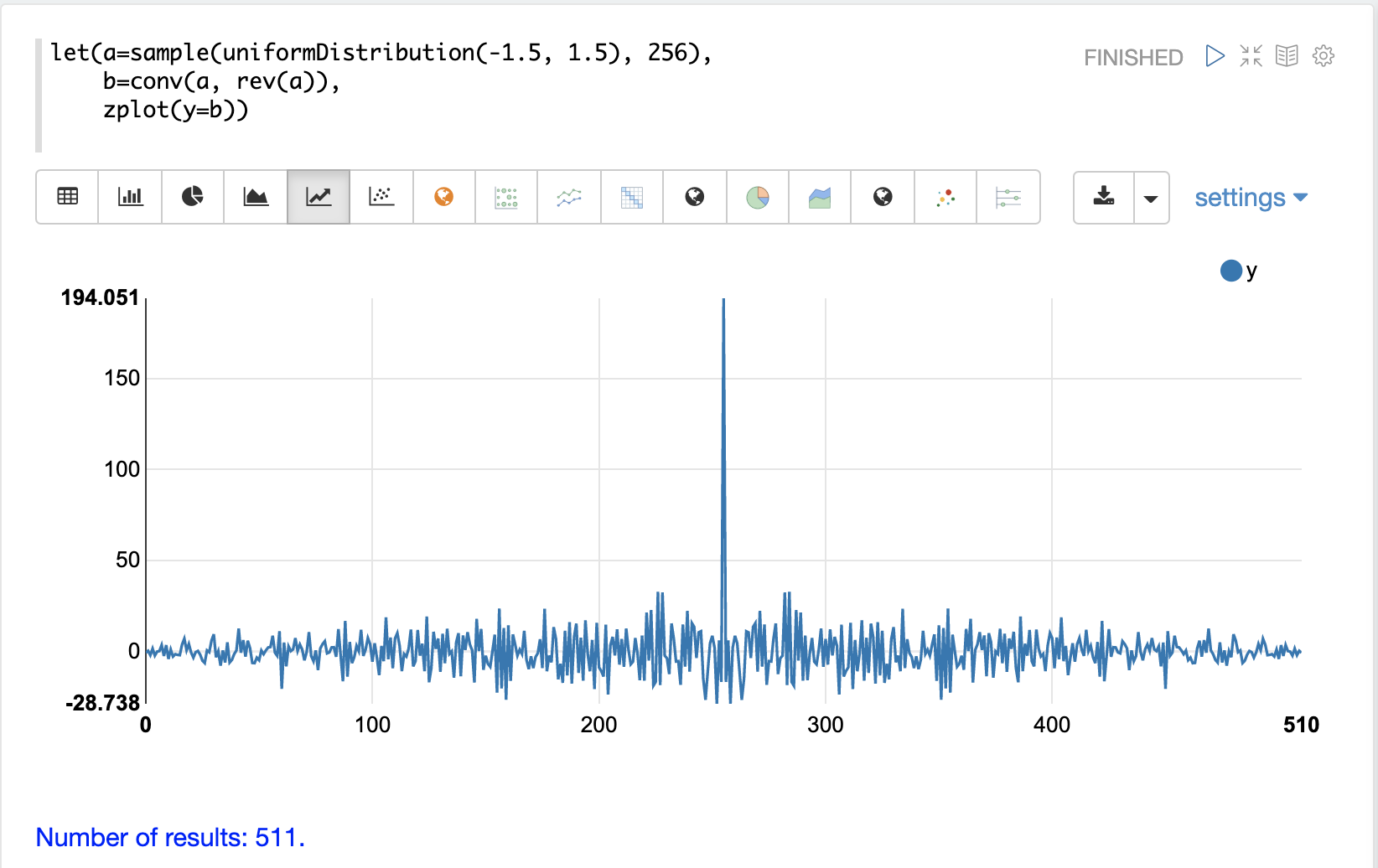
在以下範例中,會使用純雜訊向量執行自相關。請注意,自相關圖的繪圖與正弦波非常不同。在此繪圖中,有一段長時間的低強度相關性,看起來是隨機的。然後,在中心會出現一個高強度相關性的峰值,其中向量直接對齊。接著是另一段長時間的低強度相關性。
這是純雜訊的自相關圖。
在以下範例中,會對隱藏在雜訊中的正弦波向量執行自相關。請注意,此繪圖顯示非常清晰的結構跡象,與純訊號的自相關圖相似。由於雜訊的緣故,相關性較弱,但相關性圖的形狀強烈表明雜訊中隱藏著一個潛在訊號。

離散傅立葉轉換
上述基於卷積的函數是在時域中對訊號進行運算。在時域中,x 軸是時間,y 軸是特定時間點某個值的數量。
離散傅立葉轉換會將時域訊號轉換為頻域。在頻域中,x 軸是頻率,y 軸是特定頻率的累積功率。
基本原則是,每個時域訊號都是由一個或多個不同頻率的訊號(正弦波)組成。離散傅立葉轉換會將時域訊號分解為其組成頻率,並測量每個頻率的功率。
離散傅立葉轉換有許多重要的用途。在以下範例中,離散傅立葉轉換用於確定訊號是否具有結構,或者是否純粹是隨機的。
複數結果
fft 函數會對實數資料的向量執行離散傅立葉轉換。fft 函數的結果會以複數形式傳回。複數有兩個部分,實數和虛數。結果的實數部分描述了不同頻率下訊號的振幅。結果的虛數部分描述了相位。以下範例僅處理結果的實數部分。
fft 函數會傳回一個具有兩列的 matrix。矩陣中的第一列是複數結果的實數部分。矩陣中的第二列是複數結果的虛數部分。可以使用 rowAt 函數來存取列,以便將其處理為向量。
快速傅立葉轉換範例
在第一個範例中,會對自相關範例中使用的正弦波呼叫 fft 函數。
fft 函數的結果是一個矩陣。rowAt 函數用於傳回矩陣的第一列,該列是包含 fft 回應實數值的向量。
以下顯示了 fft 回應實數值的繪圖。請注意,繪圖的相對兩側有兩個峰值。該圖實際上顯示了一個鏡像回應。繪圖的右側是左側的精確鏡像。這是當 fft 在實數資料而不是複數資料上執行時的預期結果。
另請注意,fft 在單個峰值中累積了相當大的功率。這是與正弦波特定頻率相關的功率。繪圖中絕大多數頻率的相關功率都接近於 0。此 fft 顯示了一個清晰的訊號,雜訊非常低。
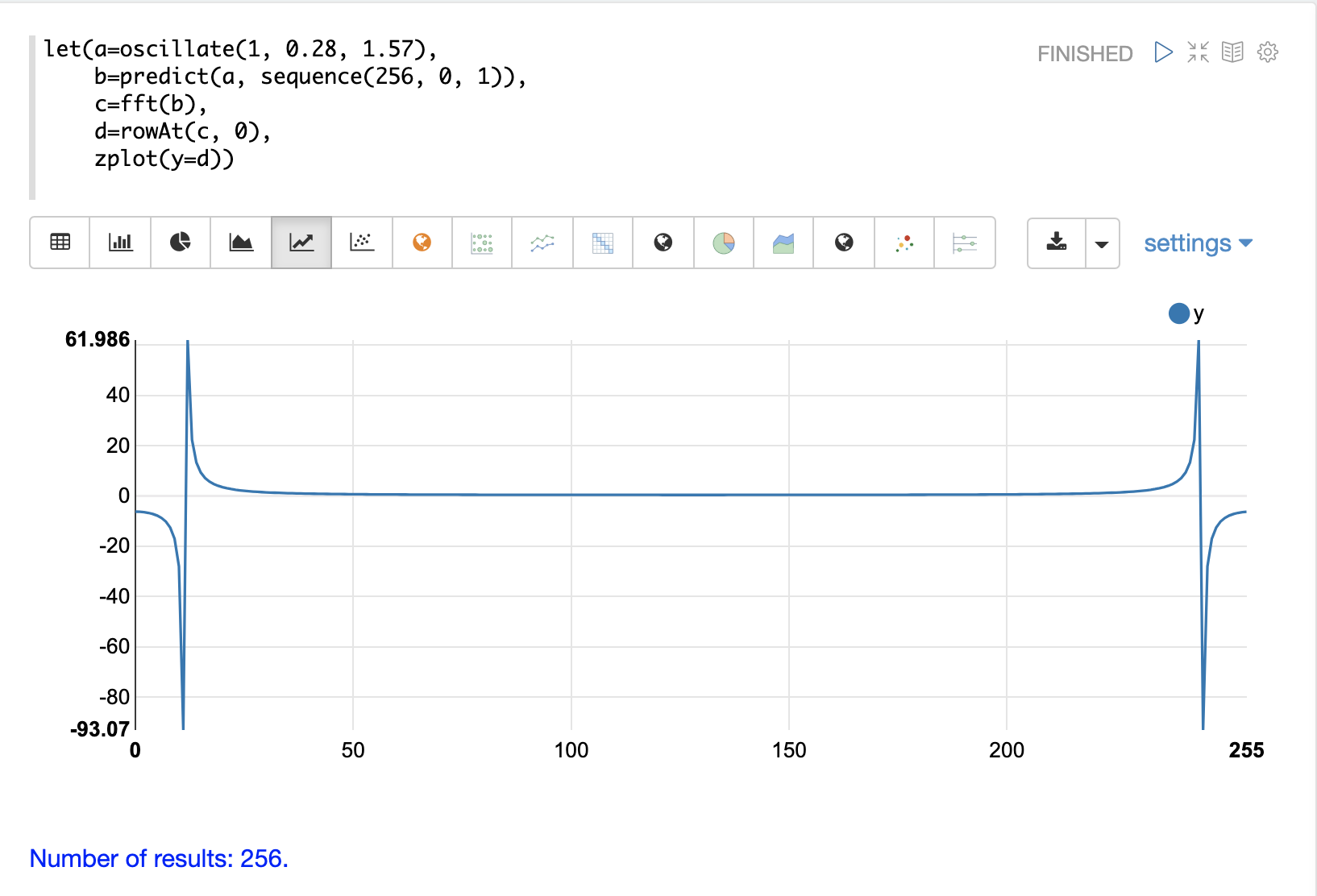
在第二個範例中,會對類似於自相關範例中使用的隨機資料向量呼叫 fft 函數。以下顯示了 fft 回應實數值的繪圖。
請注意,在此回應中,沒有明確的峰值。相反,所有頻率都累積了隨機的功率水平。此 fft 沒有顯示訊號的明確跡象,而且似乎是雜訊。
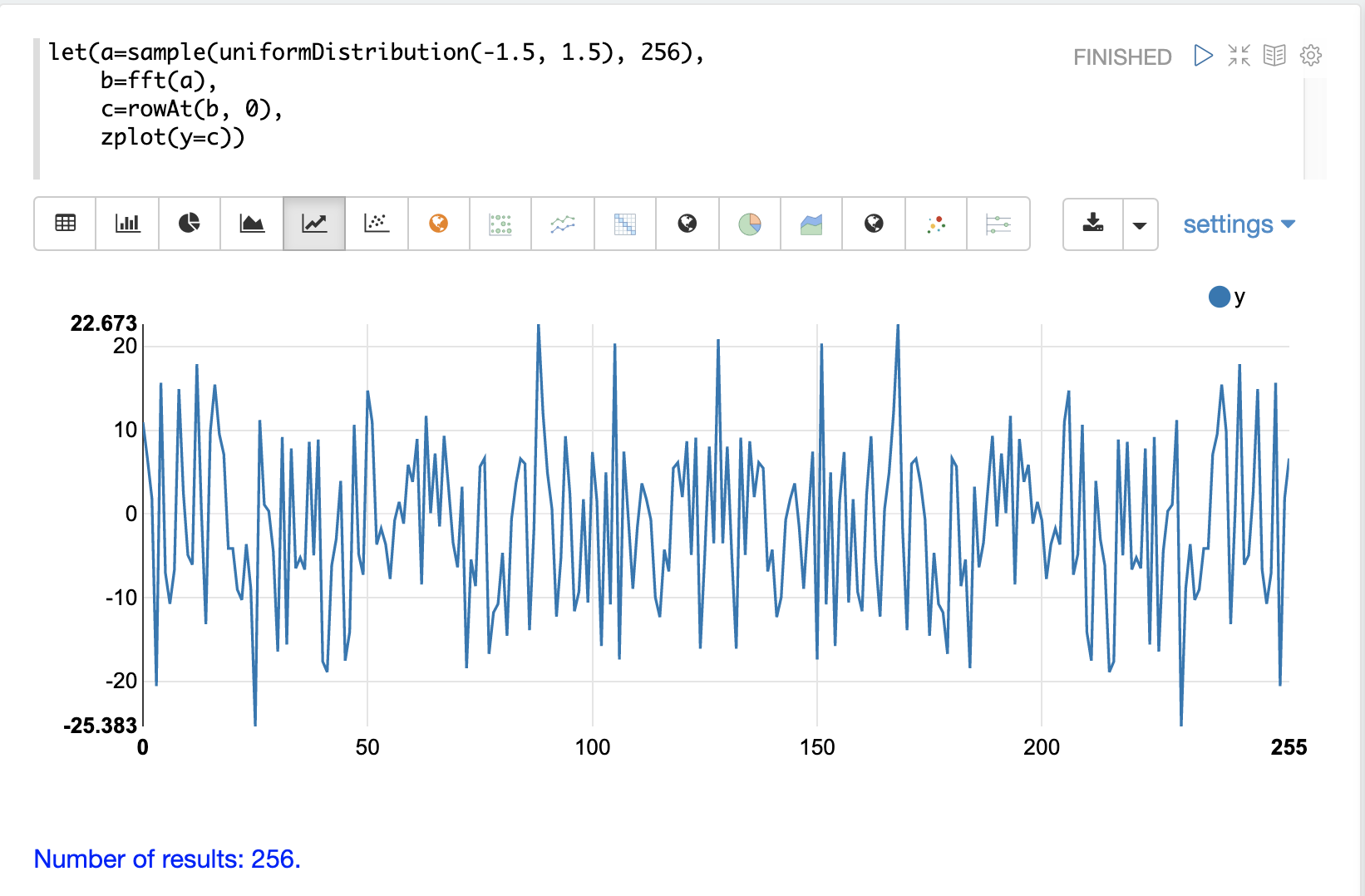
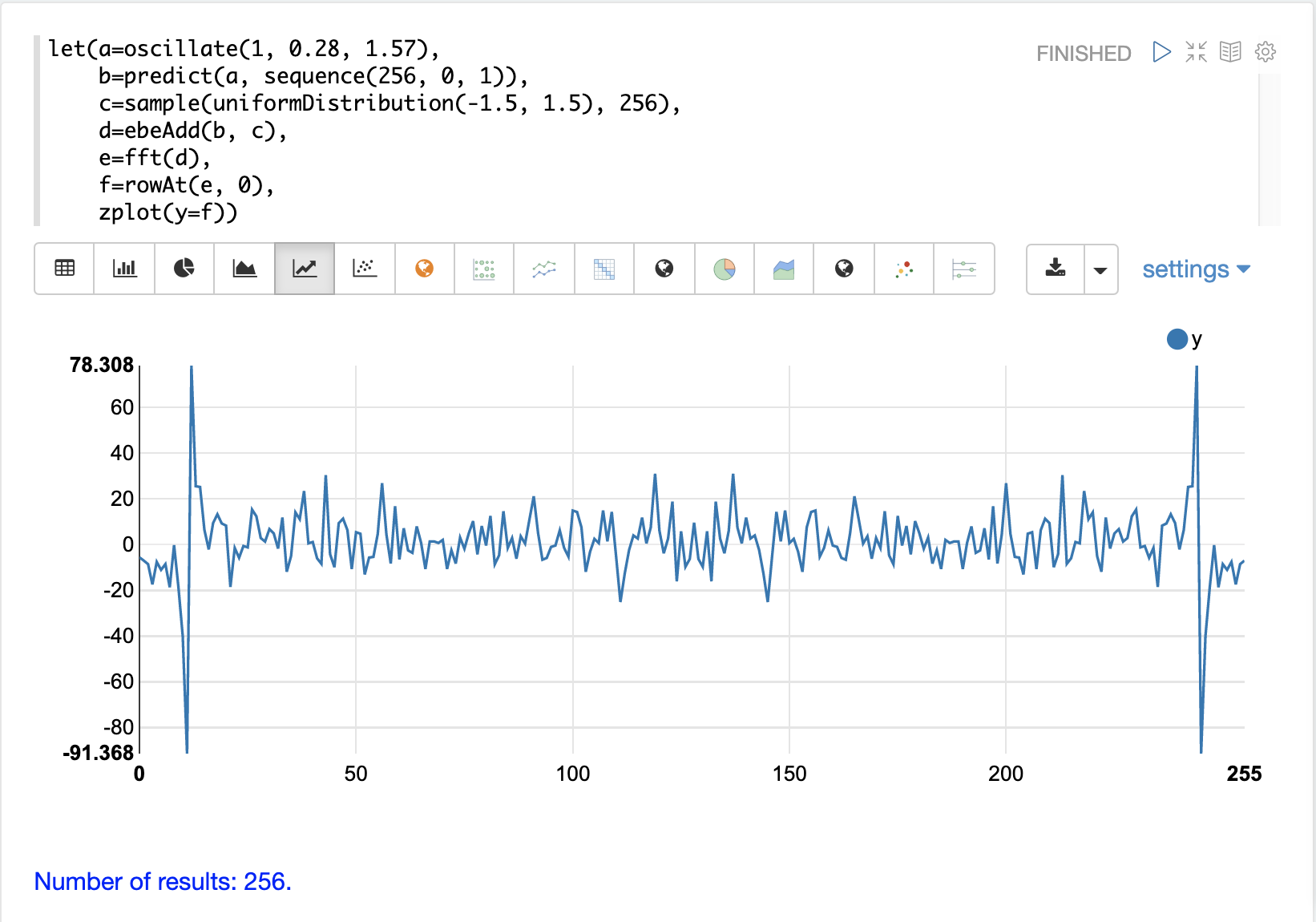
在第三個範例中,會對用於自相關範例中隱藏在雜訊中的相同訊號呼叫 fft 函數。以下顯示了 fft 回應實數值的繪圖。
請注意,有兩個清晰的鏡像峰值,其位置與純訊號的 fft 相同。但現在頻率上也存在相當大的雜訊。fft 已找到訊號,並且也顯示出訊號存在大量雜訊。