機器學習

此數學表達式使用者指南章節涵蓋機器學習函數。

距離和距離矩陣

distance 函數會計算兩個數字陣列的距離，或計算矩陣欄位的距離矩陣。

有六個距離測量函數會傳回一個執行實際距離計算的函數

euclidean (預設)
manhattan
canberra
earthMovers
cosine
haversineMeters (地理空間距離測量)

距離測量函數可以用於所有支援距離測量的機器學習函數。

以下是計算兩個數值陣列歐式距離的範例

let(a=array(20, 30, 40, 50),
    b=array(21, 29, 41, 49),
    c=distance(a, b))

當此表達式傳送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "c": 2
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

以下使用曼哈頓距離計算距離。

let(a=array(20, 30, 40, 50),
    b=array(21, 29, 41, 49),
    c=distance(a, b, manhattan()))

當此表達式傳送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "c": 4
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 1
      }
    ]
  }
}

距離矩陣

距離矩陣是視覺化兩個或多個向量之間距離的強大工具。

如果將矩陣當作參數傳遞，distance 函數會建立距離矩陣。距離矩陣是針對矩陣的欄位計算。

以下範例示範距離矩陣與二維分面結合的強大功能。

在此範例中，facet2D 函數用於產生對 nyc311 投訴資料庫中的欄位 complaint_type_s 和 zip_s 的二維分面彙總。會彙總前 20 名投訴類型和每個投訴類型的前 25 個郵遞區號。結果會是包含欄位 complaint_type_s、zip_s 和該配對計數的元組串流。

接著，使用 pivot 函數將欄位轉置成矩陣，其中 zip_s 欄位為列，而 complaint_type_s 欄位為欄。count(*) 欄位會填入矩陣儲存格中的值。

接著，使用 distance 函數，使用 cosine 距離計算矩陣欄位的距離矩陣。這會產生距離矩陣，顯示投訴類型之間基於其出現的郵遞區號的距離。

最後，使用 zplot 函數將距離矩陣繪製成熱圖。請注意，熱圖已設定為當向量之間的距離縮小時，顏色強度會增加。

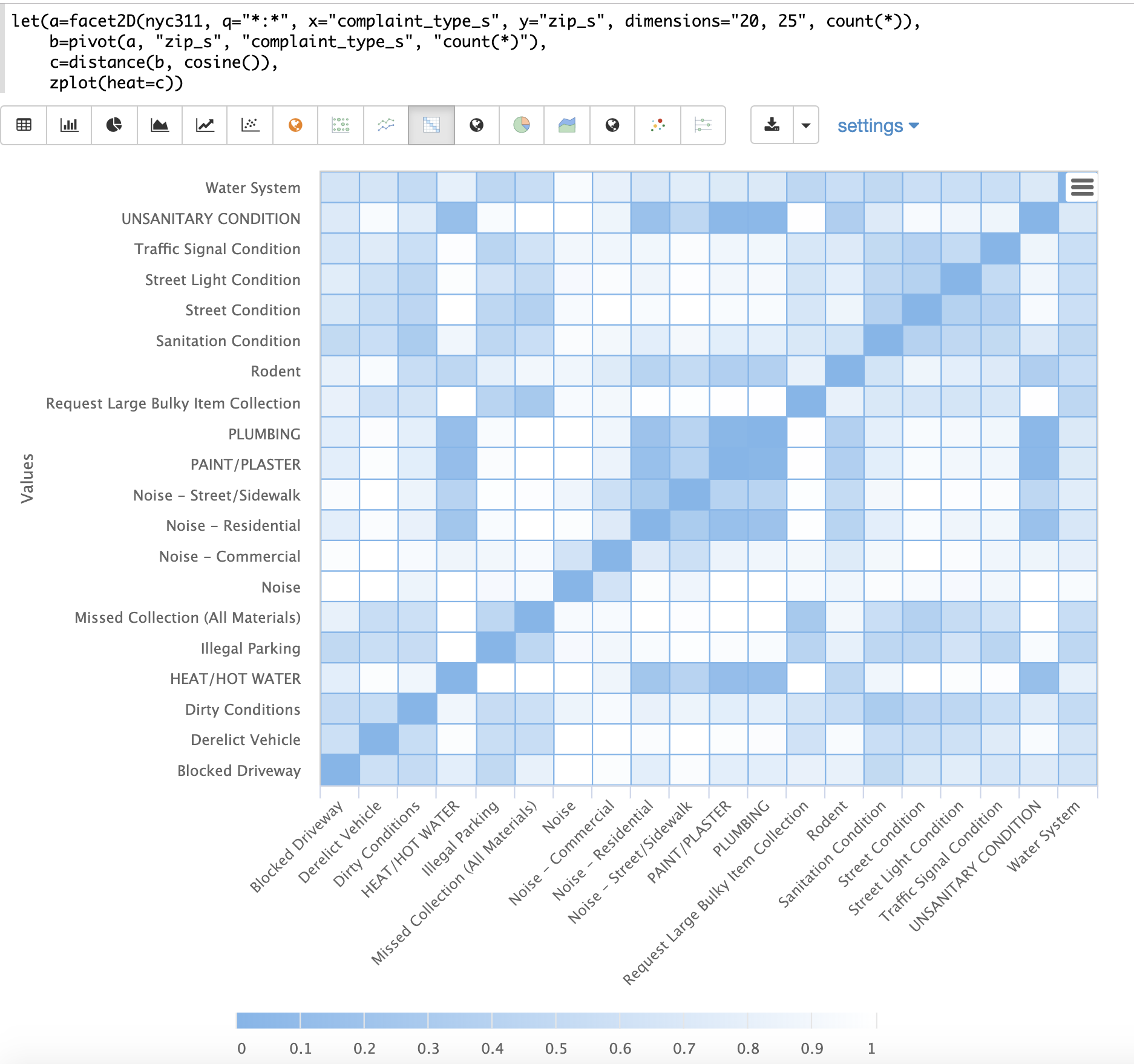
$distance$

熱圖是互動式的，因此將滑鼠移到其中一個儲存格上方，會彈出該儲存格的值。

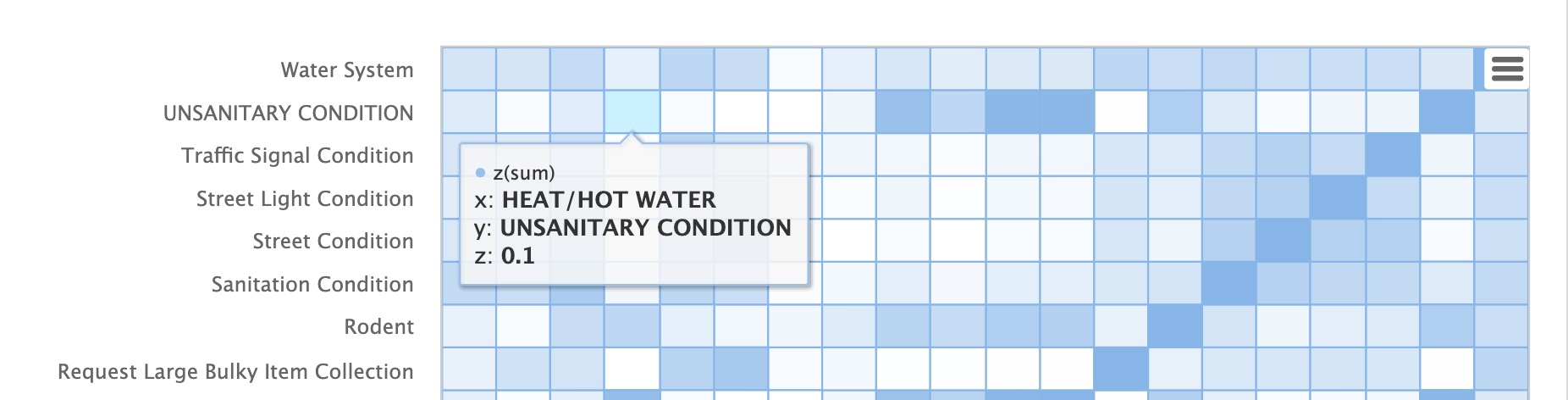
$distanceview$

請注意，HEAT/HOT WATER 和 UNSANITARY CONDITION 投訴的餘弦距離為 .1 (四捨五入到最接近的十分位)。

K 最近鄰 (KNN)

knn 函數會使用搜尋向量搜尋矩陣的列，並傳回 k 個最近鄰的矩陣。這允許在結果集上進行二次向量搜尋。

knn 函數支援透過提供下列其中一個距離測量函數來變更距離測量

euclidean (預設)
manhattan
canberra
earthMovers
cosine
haversineMeters (地理空間距離測量)

以下範例示範如何對彙總結果集執行二次搜尋。此範例的目標是找出 nyc311 投訴資料庫中，具有與郵遞區號 10280 相似的投訴類型的郵遞區號。

範例中的第一步是使用 facet2D 函數對 zip_s 和 complaint_type_s 欄位執行二維彙總。在此範例中，會計算曼哈頓行政區的前 119 個郵遞區號，以及每個郵遞區號的前 5 個投訴類型。結果是包含 zip_s、complaint_type_s 和該組合的 count(*) 的元組清單。

接著，元組列表會使用 pivot 函數樞紐分析成一個矩陣。在此範例中，pivot 函數會傳回一個以郵遞區號為行、投訴類型為列的矩陣。元組中的 count(*) 欄位會填入矩陣的儲存格。此矩陣將作為第二個搜尋矩陣。

下一步是找出 10280 郵遞區號的向量。在此範例中，這會透過三個步驟完成。第一步是使用 getRowLabels 函數從矩陣中擷取列標籤。在此情況下，列標籤是由 pivot 函數填入的郵遞區號。然後，使用 indexOf 函數找出「10280」郵遞區號在列標籤列表中的索引。接著，使用 rowAt 函數傳回矩陣中該索引的向量。此向量即為搜尋向量。

現在我們有了矩陣和搜尋向量，就可以使用 knn 函數執行搜尋。在此範例中，knn 函數使用 K 為 5 的搜尋向量搜尋矩陣，並使用餘弦距離。餘弦距離適用於比較稀疏向量，而此範例正是如此。knn 函數會傳回一個矩陣，其中包含最接近搜尋向量的前 5 個鄰近值。

knn 函數會填入傳回矩陣的行和列標籤，並將每個列的距離向量做為屬性新增至矩陣。

在此範例中，zplot 函數會使用 getRowLabels 和 getAttribute 函數擷取列標籤和距離向量。topFeatures 函數會根據每個資料行的計數，擷取每個郵遞區號向量的前 5 個資料行標籤。然後，zplot 會以可以在 Zeppelin-Solr 表格中視覺化的格式輸出資料。

$knn$

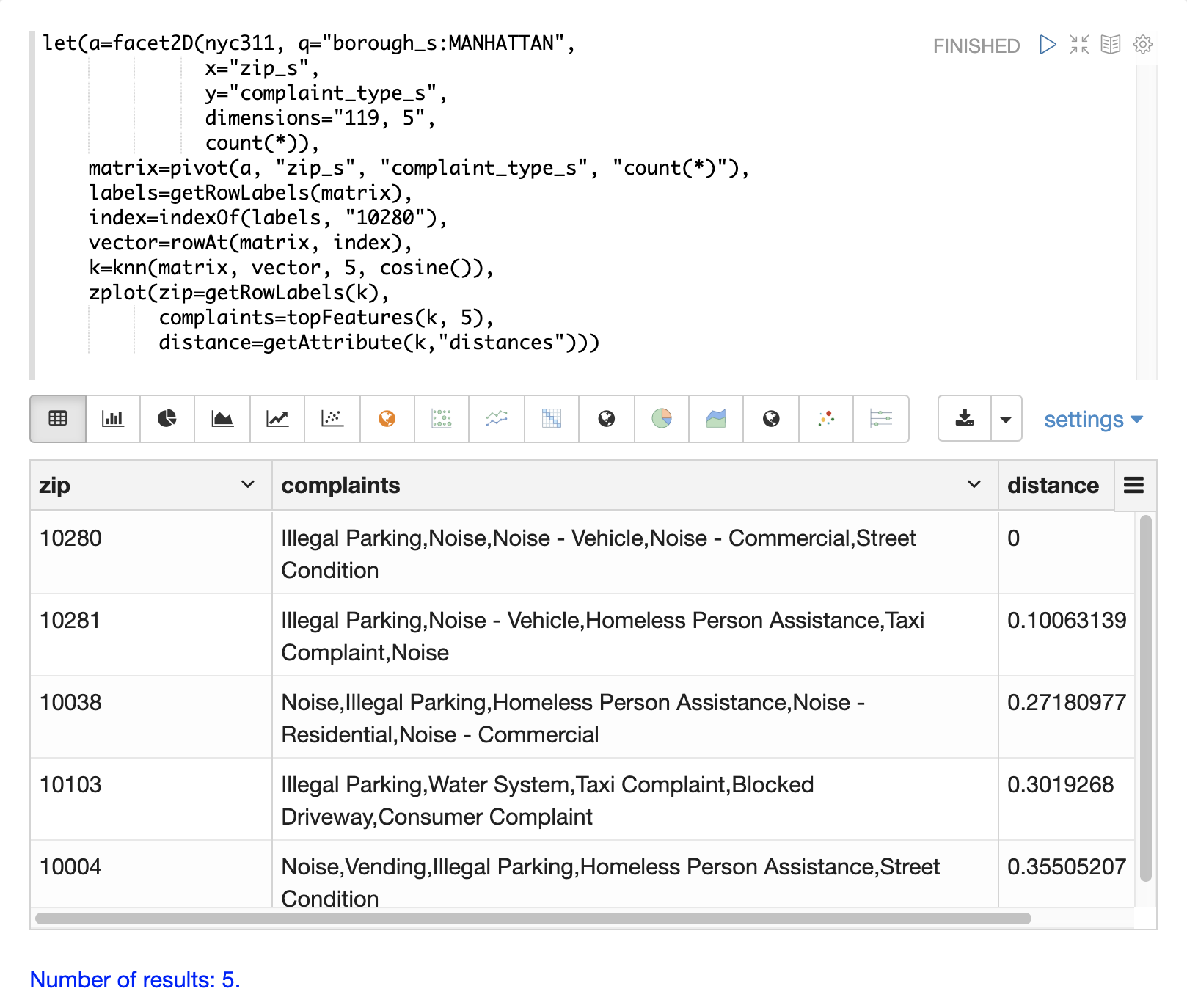
上表顯示 knn 函數傳回的每個郵遞區號，以及投訴列表和距離。這些是根據前 5 項投訴類型，與 10280 郵遞區號最相似的郵遞區號。

K 最近鄰迴歸

K 最近鄰迴歸是一種非線性、雙變數和多變數迴歸方法。KNN 迴歸是一種惰性學習技術，這表示它不會事先將模型擬合到訓練集。相反地，整個觀察值和結果的訓練集都保存在記憶體中，並且透過平均 k 個最近鄰的結果來進行預測。

knnRegress 函數用於執行最近鄰迴歸。

2D 非線性迴歸

以下範例顯示套用至 2D 散佈圖的 KNN 迴歸的迴歸圖。

在此範例中，random 函數用於從包含兩個欄位 filesize_d 和 eresponse_d 的 logs 集合中繪製 500 個隨機樣本。然後，樣本會向量化，其中 filesize_d 欄位儲存在指定給變數 x 的向量中，而 eresponse_d 向量儲存在變數 y 中。接著，將 knnRegress 函數套用參數為 20 的最近鄰，傳回一個可用於預測值的 KNN 函數。然後，在 KNN 函數上呼叫 predict 函數，以預測原始 x 向量的值。最後，使用 zplot 繪製原始 x 和 y 向量以及預測值。

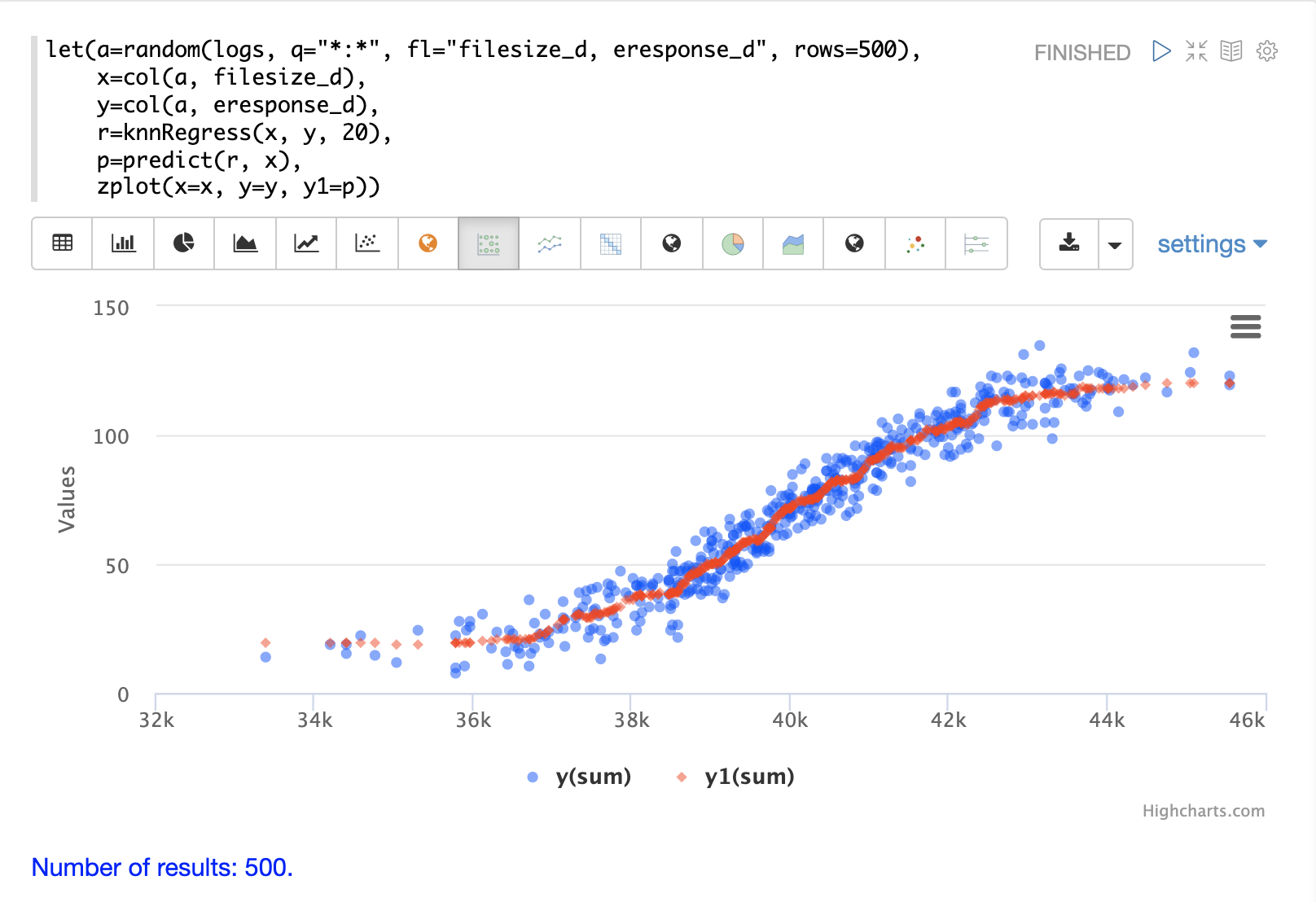
$knnRegress$

請注意，迴歸圖顯示 filesize_d 欄位和 eresponse_d 欄位之間的非線性關係。另請注意，KNN 迴歸會在散佈圖中繪製一條非線性曲線。K (最近鄰) 的大小越大，線條越平滑。

多變數非線性迴歸

knnRegress 函數也是多變數非線性迴歸的強大且靈活的工具。

在以下範例中，會使用專為分析和預測葡萄酒品質而設計的資料庫執行多變數迴歸。資料庫包含近 1600 筆記錄，其中包含 9 個葡萄酒品質預測指標：pH 值、酒精含量、固定酸度、硫酸鹽含量、密度、游離二氧化硫含量、揮發性酸度、檸檬酸含量、殘糖量。還有一個名為品質的欄位，指定給每種葡萄酒，範圍從 3 到 8。

KNN 迴歸可用於預測包含預測值向量的葡萄酒品質。

在此範例中，會在 redwine 集合上執行搜尋，以傳回觀察資料庫中的所有列。然後，品質欄位和預測欄位會讀入向量並設定為變數。

預測變數會新增為矩陣的列，並轉置以使矩陣中的每一列都包含一個具有 9 個預測值的觀察值。這是我們的觀察矩陣，並指定給變數 obs。

然後，knnRegress 函數會使用品質結果迴歸觀察值。在此範例中，K 的值設定為 5，因此將使用 5 個最近鄰的平均品質來計算品質。

然後，使用 predict 函數為整個觀察集產生預測向量。這些預測將用於判斷 KNN 迴歸在觀察資料上的執行效果。

然後，透過從觀察到的品質中減去預測的品質，計算迴歸的誤差或殘差。ebeSubtract 函數用於在兩個向量之間執行逐元素減法。

最後，zplot 函數會格式化預測和誤差，以便視覺化殘差圖。

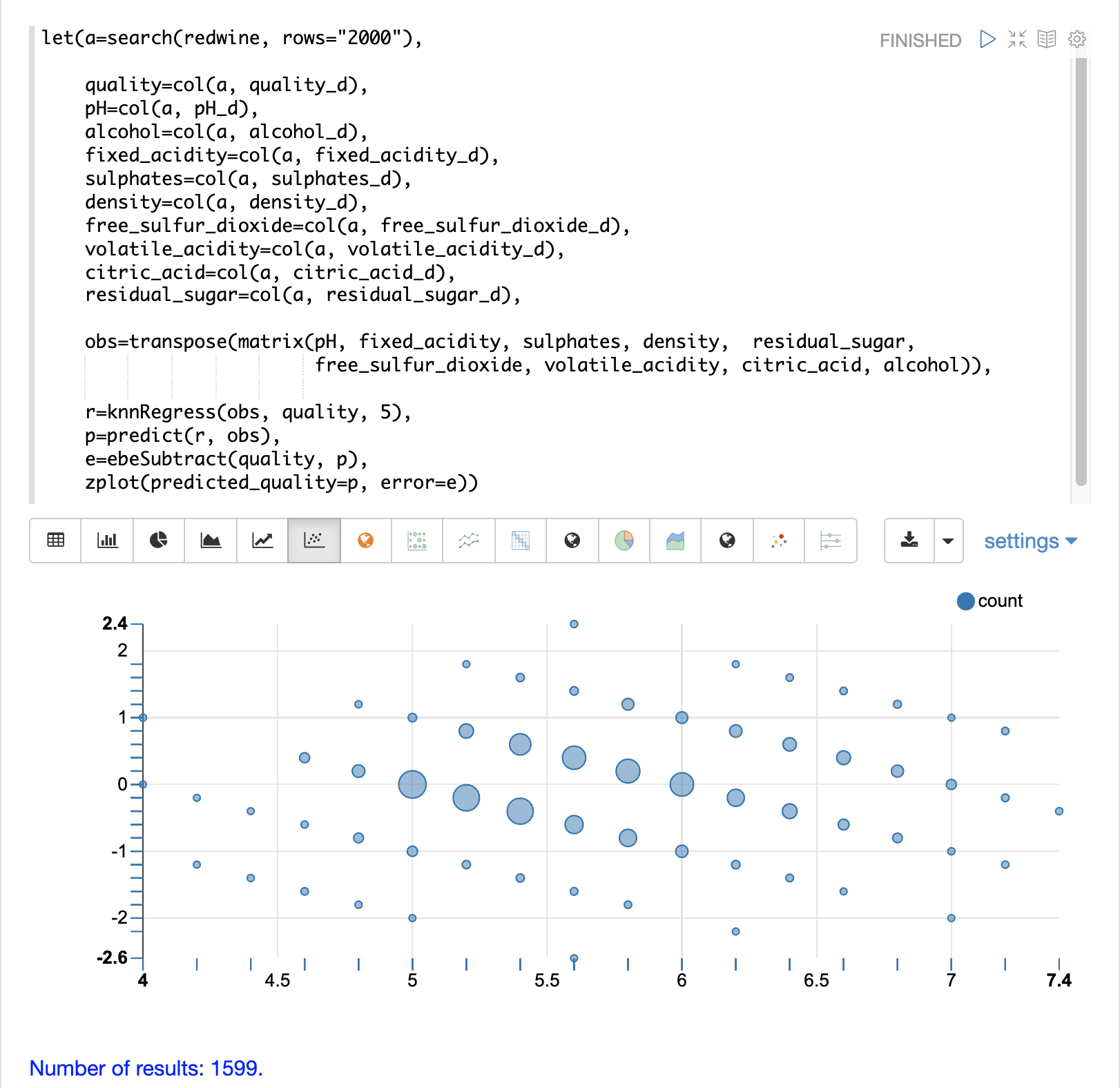
$redwine1$

殘差圖會在 x 軸上繪製預測的值，並在 y 軸上繪製預測的誤差。散佈圖顯示誤差如何在整個預測範圍內分佈。

可以解釋殘差圖以了解 KNN 迴歸在訓練資料上的執行效果。

該圖顯示預測誤差似乎相當均勻地分佈在零以上和以下。隨著誤差接近零，誤差的密度會增加。氣泡大小會反映繪圖中特定點的誤差密度。這提供了模型誤差分佈的直觀感覺。
該圖也會視覺化整個預測範圍內誤差的變異數。這提供了直觀的理解，即 KNN 預測是否會在整個範圍預測中具有相似的誤差變異數。

也可以使用直方圖視覺化殘差，以便更好地了解殘差分佈的形狀。以下範例顯示與上述相同的 KNN 迴歸，並繪製誤差分佈圖。

在此範例中，zplot 函數用於繪製殘差的 empiricalDistribution 函數圖，並使用 11 個間隔的直方圖。

$redwine2$

請注意，誤差遵循以接近 0 為中心的鐘形曲線。從此圖中，我們可以看到獲得介於 -1 和 1 之間的預測誤差的機率很高。

其他 KNN 迴歸參數

knnRegression 函數具有三個額外參數，使其適用於許多不同的迴歸案例。

任何距離測量都可以用於迴歸，只需將函數新增至呼叫即可。這允許在稀疏向量 (cosine)、密集向量和地理空間經緯度向量 (haversineMeters) 上進行迴歸分析。

範例語法
```
r=knnRegress(obs, quality, 5, cosine()),
```
robust 具名參數可用於執行對結果中的離群值具有穩健性的迴歸分析。使用 robust 參數時，會使用 k 個最近鄰的中位數結果，而不是平均值。

範例語法
```
r=knnRegress(obs, quality, 5, robust="true"),
```
scale 具名參數可用於在預測時縮放觀察值和搜尋向量的資料行。當特徵資料行位於不同尺度時，這可以改善 KNN 迴歸的效能，這會導致距離計算對較大的資料行施加過多的權重。

範例語法
```
r=knnRegress(obs, quality, 5, scale="true"),
```

knnSearch

knnSearch 函數會根據文字相似度傳回文件的 k 個最近鄰。在底層，knnSearch 函數使用 Solr 的 More Like This 查詢剖析器。此功能使用搜尋引擎的查詢、詞彙統計資料、評分和排名功能，以在大型分散式索引中快速執行相似文件的最近鄰搜尋。

此搜尋的結果可以直接使用，或為機器學習運算 (例如第二個 KNN 向量搜尋) 提供候選項目。

以下範例顯示電影評論資料集上的 knnSearch 函數。此搜尋會根據 review_t 欄位的相似度，傳回與特定文件 ID (83e9b5b0…) 最相似的 50 個文件。mindf 和 maxdf 指定用於執行搜尋的詞彙的最小和最大文件頻率。這些參數可以透過消除高頻率詞彙來加快查詢速度，並透過從搜尋中移除雜訊詞彙來提高精確度。

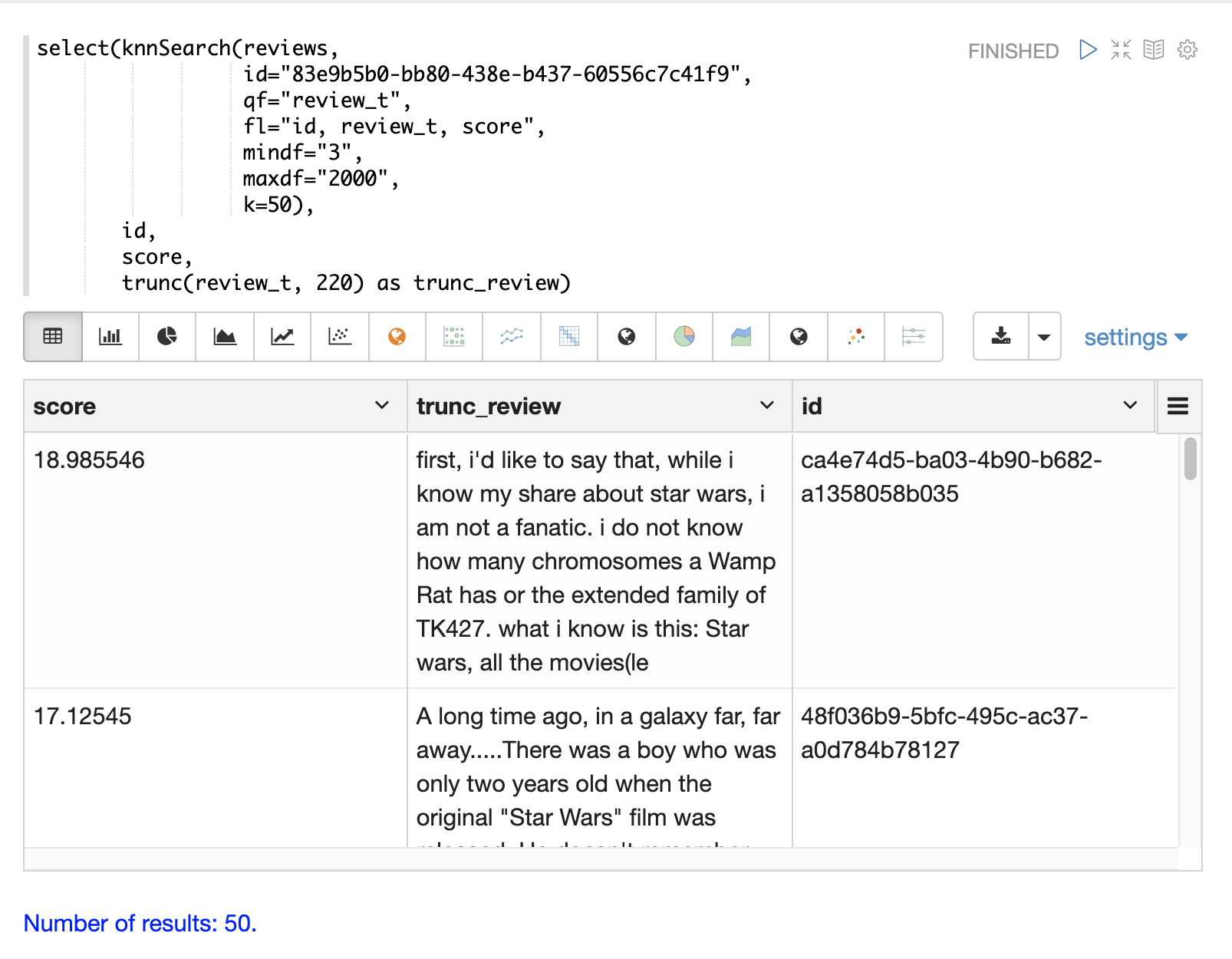
$knnSearch$

在此範例中，使用 select 函數來截斷輸出中的評論，使其成為 220 個字元，以便在表格中更易於閱讀。

DBSCAN

DBSCAN 叢集是一種強大的密度式叢集演算法，特別適用於地理空間叢集。DBSCAN 使用兩個參數來篩選結果集，使其成為特定密度的叢集

eps (Epsilon)：定義被視為鄰居的點之間的距離
min 點：叢集中要傳回的點的最小數目。

2D 叢集視覺化

zplot 函數透過使用 clusters 具名參數直接支援繪製 2D 叢集。

以下範例使用 DBSCAN 叢集和叢集視覺化，以在 NYC 311 投訴資料庫的地圖上找出老鼠出沒的熱點。

在此範例中，random 函數會從 nyc311 集合中繪製記錄樣本，其中投訴描述符合「老鼠出沒」，且記錄中填入緯度。然後，將緯度和經度欄位向量化並新增為矩陣的列。轉置矩陣，以便每列都包含單個緯度、經度點。然後，使用 dbscan 函數來叢集緯度和經度點。請注意，範例中的 dbscan 函數有四個參數。

obs：緯度/經度點的觀察矩陣
eps：被視為一個群集的點之間的距離。範例中為 100 公尺。
min points：一個群集中要被函式回傳的最小點數。範例中為 5。
distance measure：一個可選的距離度量，用於判斷點之間的距離。預設值為歐幾里得距離。範例使用 haversineMeters，它會回傳以公尺為單位的距離，對於地理空間用例來說更有意義。

最後，zplot 函式用於在 Zeppelin-Solr 的地圖上視覺化群集。下方的地圖已縮放到布魯克林一個鼠患通報高密度的特定區域。

$dbscan1$

請注意，在視覺化中，從 5000 個樣本中僅回傳了 1019 個點。這就是 DBSCAN 演算法過濾不符合群集條件的記錄的能力。繪製的點都屬於明確定義的群集。

可以進一步縮放地圖視覺化，以探索特定群集的位置。下方的範例顯示縮放到密集群集區域的情況。

$dbscan2$

K-均值群集

kmeans 函式對矩陣的列執行 K-均值群集。完成群集後，可以使用許多有用的函式來檢查和視覺化群集和質心。

群集散佈圖

在此範例中，我們將再次對鼠患通報的 2D 經緯度點進行群集。但與 DBSCAN 範例不同的是，K-均值群集本身不會執行任何雜訊減少。因此，為了減少雜訊，從資料中選取比 DBSCAN 範例中使用的更小的隨機樣本。

我們將會看到，取樣本身是一種強大的雜訊減少工具，有助於視覺化群集密度。這是因為從較高密度群集中抽樣的機率較高，而從較低密度群集中抽樣的機率較低。

在此範例中，random 函式從 nyc311（投訴資料庫）集合中抽取 1500 筆記錄的樣本，其中投訴描述符合「rat sighting」且記錄中已填入緯度。然後將緯度和經度欄位向量化，並作為列新增至矩陣。轉置矩陣，使每一列都包含單一的經緯度點。然後使用 kmeans 函式將經緯度點群集到 21 個群集中。最後，使用 zplot 函式將群集視覺化為散佈圖。

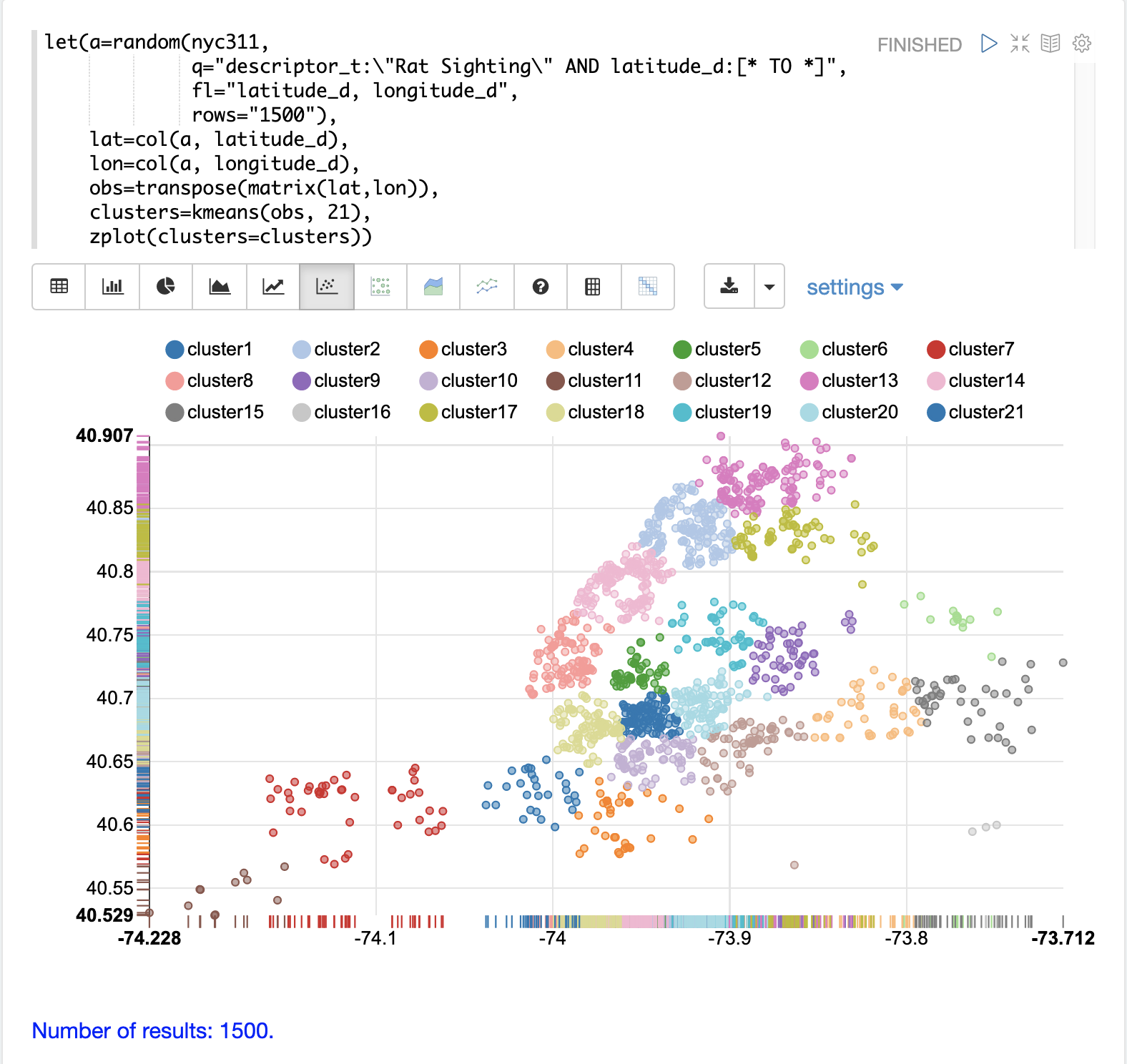
$2DCluster1$

上方的散佈圖顯示每個經緯度點都繪製在歐幾里得平面上，經度在 x 軸上，緯度在 y 軸上。該圖的密度足夠高，如果您了解紐約市的行政區，則可以看到不同行政區的輪廓。

每個群集都以不同的顏色顯示。此圖提供了關於整個紐約市五個行政區鼠患通報密度的有趣見解。例如，它突顯了布魯克林 cluster1 中密集的通報群集，以及周圍密度較低但活動仍然很高的群集。

繪製質心

然後可以在地圖上繪製每個群集的質心，以視覺化群集的中心。在下方的範例中，使用 getCentroids 函式從群集中提取質心，該函式會回傳質心的矩陣。

質心矩陣包含 2D 經緯度點。然後可以使用 colAt 函式從矩陣中按索引提取緯度和經度欄位，以便可以使用 zplot 繪製它們。下方使用地圖視覺化來顯示質心。

$centroidplot$

然後可以縮放地圖，以便更仔細地查看群集散佈圖中顯示的高密度區域中的質心。

$centroidzoom$

片語提取

K-均值群集會產生質心或原型向量，可用於表示每個群集。在此範例中，將提取質心的關鍵特徵，以表示 TF-IDF 詞向量的群集的關鍵片語。

下方的範例使用 TF-IDF 詞向量。「文字分析和詞向量」章節提供了對這些特徵的完整說明。

在範例中，search 函式會回傳 review_t 欄位符合片語「star wars」的文件。在結果集上執行 select 函式，並套用 analyze 函式，該函式使用附加到架構欄位 text_bigrams 的分析器來重新分析 review_t 欄位。此分析器會回傳雙字詞，然後將其註釋到名為 terms 的欄位中的文件中。

然後 termVectors 函式會從儲存在 terms 欄位中的雙字詞建立 TD-IDF 詞向量。然後使用 kmeans 函式將雙字詞詞向量群集到 5 個群集中。最後，從質心中提取前 5 個特徵並回傳。請注意，這些特徵都是具有語義意義的雙字詞片語。

let(a=select(search(reviews, q="review_t:\"star wars\"", rows="500"),
             id,
             analyze(review_t, text_bigrams) as terms),
    vectors=termVectors(a, maxDocFreq=.10, minDocFreq=.03, minTermLength=13, exclude="_,br,have"),
    clusters=kmeans(vectors, 5),
    centroids=getCentroids(clusters),
    phrases=topFeatures(centroids, 5))

當此表達式傳送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "phrases": [
          [
            "empire strikes",
            "rebel alliance",
            "princess leia",
            "luke skywalker",
            "phantom menace"
          ],
          [
            "original star",
            "main characters",
            "production values",
            "anakin skywalker",
            "luke skywalker"
          ],
          [
            "carrie fisher",
            "original films",
            "harrison ford",
            "luke skywalker",
            "ian mcdiarmid"
          ],
          [
            "phantom menace",
            "original trilogy",
            "harrison ford",
            "john williams",
            "empire strikes"
          ],
          [
            "science fiction",
            "fiction films",
            "forbidden planet",
            "character development",
            "worth watching"
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 46
      }
    ]
  }
}

多重 K-均值群集

K-均值群集會根據質心的初始位置產生不同的結果。K-均值的速度夠快，可以執行多次試驗，以便選取最佳結果。

multiKmeans 函式會執行指定次數試驗的 K-均值群集演算法，並根據哪個試驗產生最低的群內變異數來選取最佳結果。

下方的範例與片語提取範例相同，不同之處在於它使用 multiKmeans 執行 15 次試驗，而不是 kmeans 函式的單次試驗。

let(a=select(search(reviews, q="review_t:\"star wars\"", rows="500"),
             id,
             analyze(review_t, text_bigrams) as terms),
    vectors=termVectors(a, maxDocFreq=.10, minDocFreq=.03, minTermLength=13, exclude="_,br,have"),
    clusters=multiKmeans(vectors, 5, 15),
    centroids=getCentroids(clusters),
    phrases=topFeatures(centroids, 5))

此表達式會回傳以下回應

{
  "result-set": {
    "docs": [
      {
        "phrases": [
          [
            "science fiction",
            "original star",
            "production values",
            "fiction films",
            "forbidden planet"
          ],
          [
            "empire strikes",
            "princess leia",
            "luke skywalker",
            "phantom menace"
          ],
          [
            "carrie fisher",
            "harrison ford",
            "luke skywalker",
            "empire strikes",
            "original films"
          ],
          [
            "phantom menace",
            "original trilogy",
            "harrison ford",
            "character development",
            "john williams"
          ],
          [
            "rebel alliance",
            "empire strikes",
            "princess leia",
            "original trilogy",
            "luke skywalker"
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 84
      }
    ]
  }
}

模糊 K-均值群集

fuzzyKmeans 函式是一種軟群集演算法，允許將向量指派給多個群集。fuzziness 參數是介於 1 和 2 之間的值，用於決定群集指派的模糊程度。

執行群集後，可以在群集結果上呼叫 getMembershipMatrix 函式，以回傳描述每個向量的群集成員資格機率的矩陣。此矩陣可用於了解群集之間的關係。

在下方的範例中，fuzzyKmeans 用於對符合片語「star wars」的電影評論進行群集。但不是查看群集或質心，而是使用 getMembershipMatrix 來回傳每個文件的成員資格機率。成員資格矩陣由已群集的每個向量的列組成。矩陣中每個群集都有一個欄位。矩陣中的值包含特定向量屬於特定群集的機率。

在範例中，然後使用 distance 函式從成員資格矩陣的欄位建立距離矩陣。然後使用 zplot 函式將距離矩陣視覺化為熱圖。

在範例中，cluster1 和 cluster5 的群集之間的距離最短。可以執行這兩個群集中的特徵的進一步分析，以了解 cluster1 和 cluster5 之間的關係。

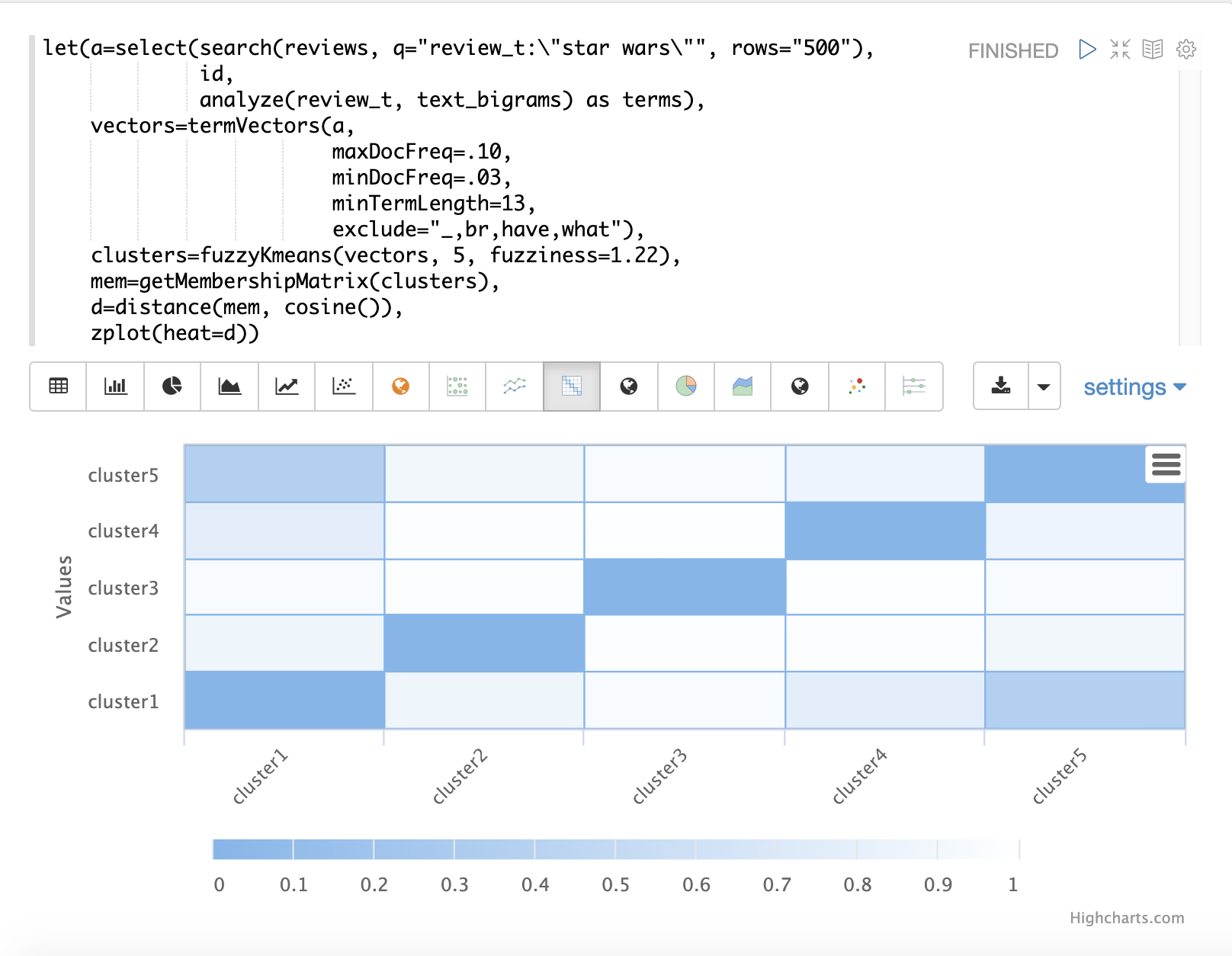
$fuzzyk$

熱圖已設定為隨著距離縮短而增加顏色強度。

特徵縮放

在執行機器學習運算之前，通常需要縮放特徵向量，以便可以在相同的尺度上進行比較。

下方所有的縮放函式都在向量和矩陣上運作。在矩陣上運作時，會縮放矩陣的列。

最小值/最大值縮放

minMaxScale 函式會在最小值和最大值之間縮放向量或矩陣。預設情況下，如果未提供最小值/最大值，則會在 0 和 1 之間縮放。

下方是振幅為 1 的正弦波在縮放到 -5 到 5 之間之前和之後的圖。

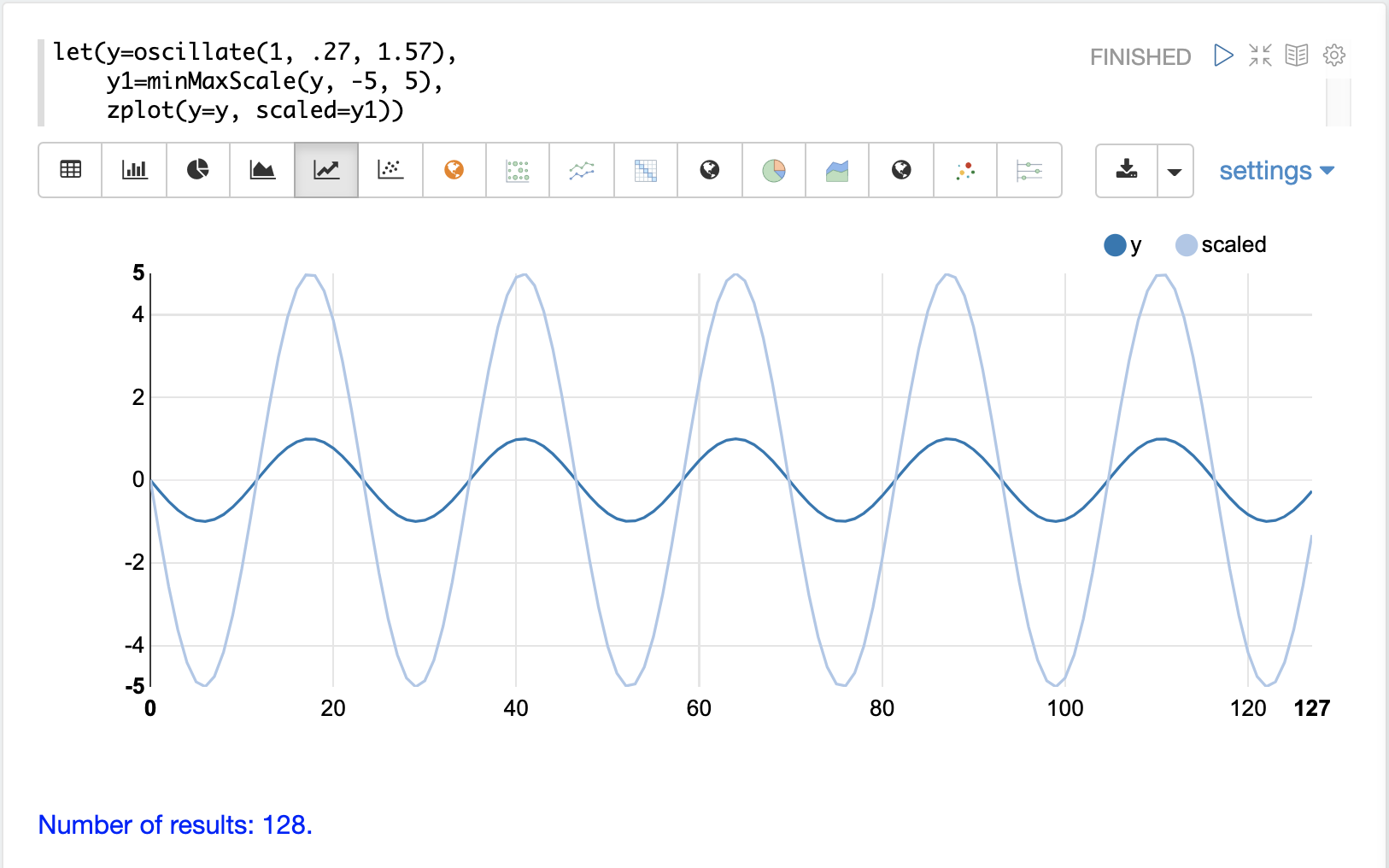
$minmaxscale$

下方是在 0 到 1 之間縮放矩陣的簡單最小值/最大值縮放範例。請注意，一旦引入相同的尺度，向量就會相同。

let(a=array(20, 30, 40, 50),
    b=array(200, 300, 400, 500),
    c=matrix(a, b),
    d=minMaxScale(c))

當此表達式傳送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "d": [
          [
            0,
            0.3333333333333333,
            0.6666666666666666,
            1
          ],
          [
            0,
            0.3333333333333333,
            0.6666666666666666,
            1
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

標準化

standardize 函式會縮放向量，使其平均值為 0，標準差為 1。

下方是振幅為 1 的正弦波在標準化之前和之後的圖。

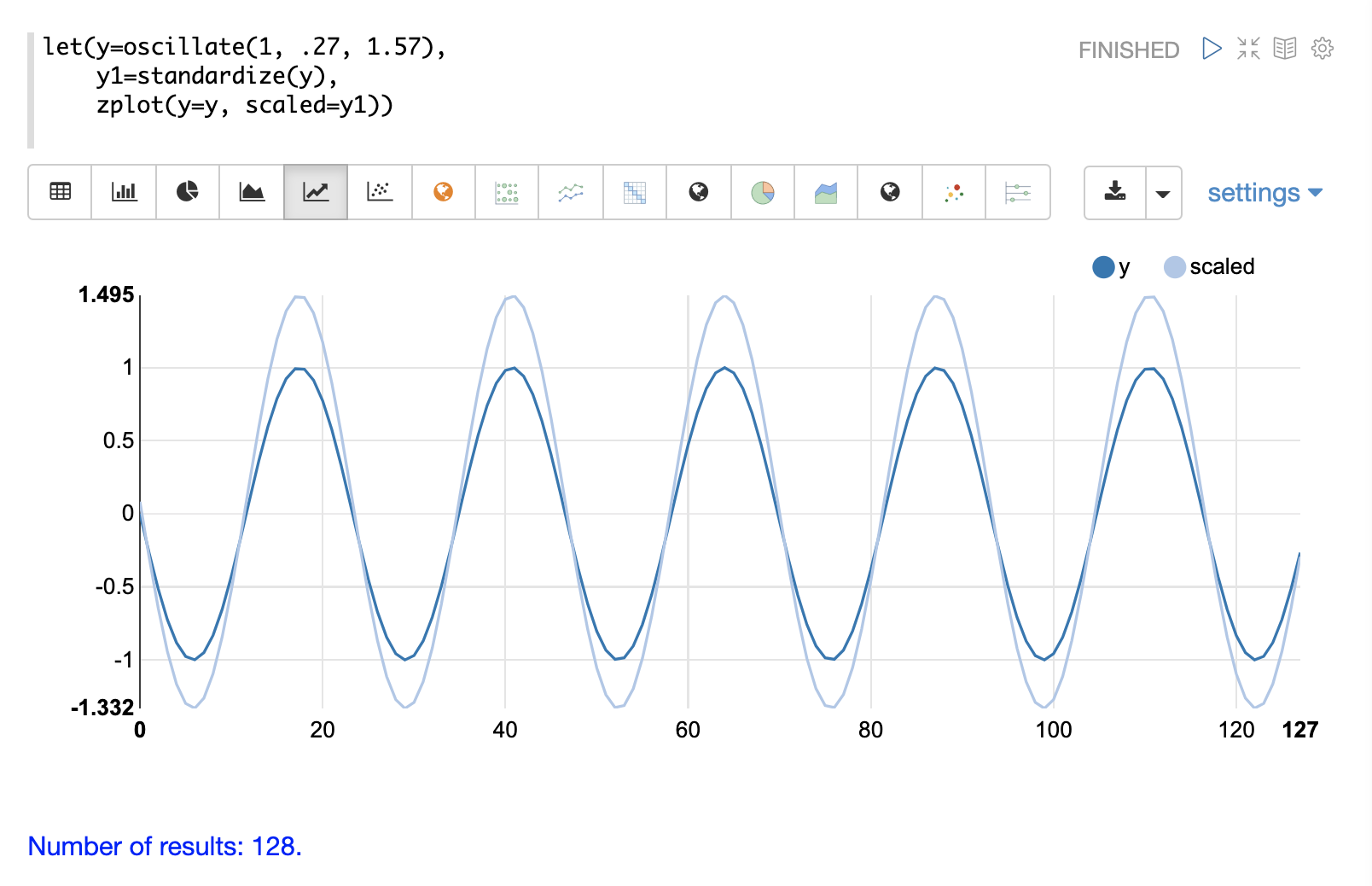
$standardize$

下方是標準化矩陣的簡單範例。請注意，一旦引入相同的尺度，向量就會相同。

let(a=array(20, 30, 40, 50),
    b=array(200, 300, 400, 500),
    c=matrix(a, b),
    d=standardize(c))

當此表達式傳送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "d": [
          [
            -1.161895003862225,
            -0.3872983346207417,
            0.3872983346207417,
            1.161895003862225
          ],
          [
            -1.1618950038622249,
            -0.38729833462074165,
            0.38729833462074165,
            1.1618950038622249
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 17
      }
    ]
  }
}

單位向量

unitize 函式會將向量縮放為大小 1。大小為 1 的向量稱為單位向量。當向量數學處理的是向量方向而不是大小時，最好使用單位向量。

下方是振幅為 1 的正弦波在單位化之前和之後的圖。

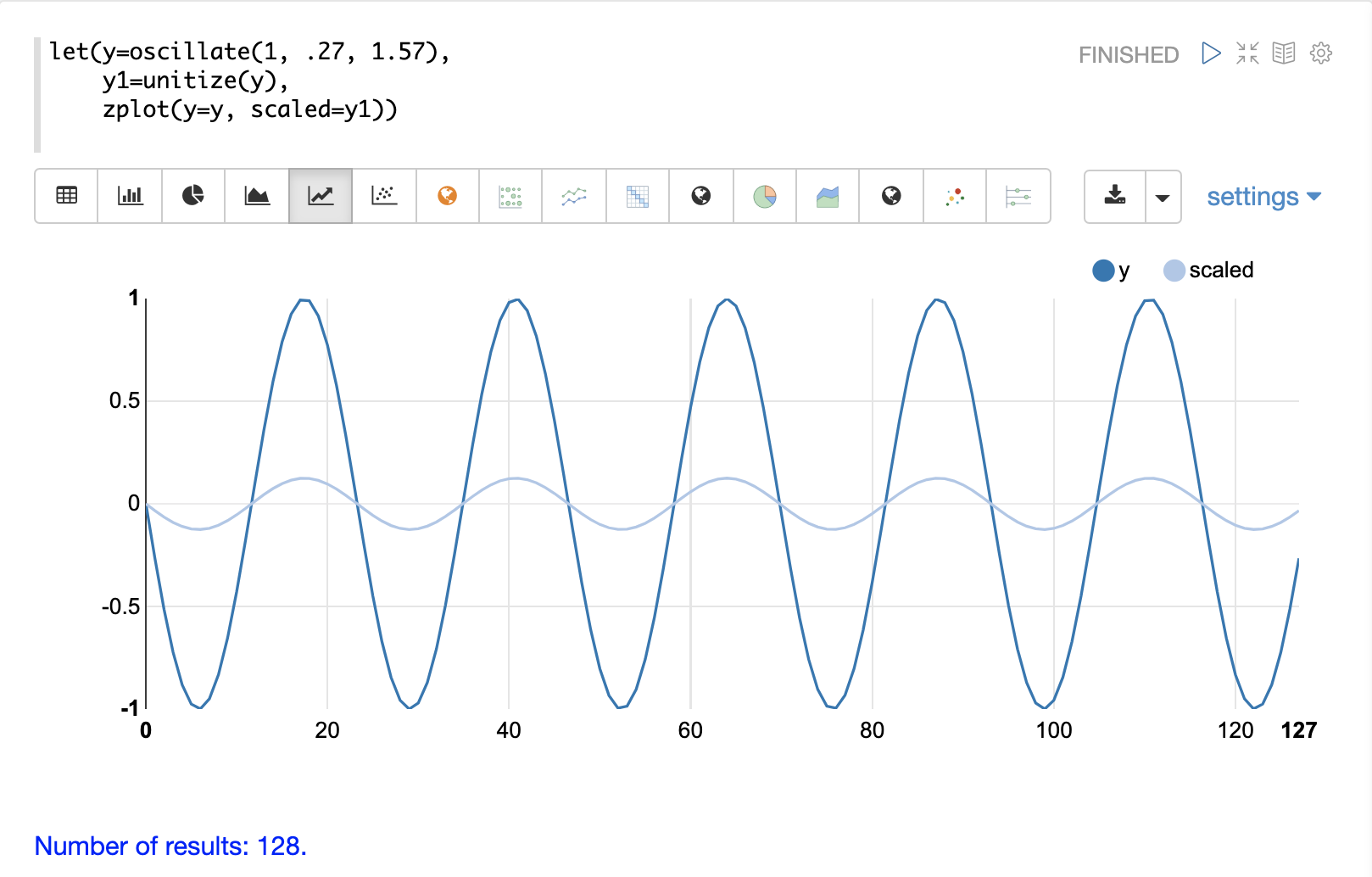
$unitize$

下方是單位化矩陣的簡單範例。請注意，一旦引入相同的尺度，向量就會相同。

let(a=array(20, 30, 40, 50),
    b=array(200, 300, 400, 500),
    c=matrix(a, b),
    d=unitize(c))

當此表達式傳送到 /stream 處理器時，它會回應

{
  "result-set": {
    "docs": [
      {
        "d": [
          [
            0.2721655269759087,
            0.40824829046386296,
            0.5443310539518174,
            0.6804138174397716
          ],
          [
            0.2721655269759087,
            0.4082482904638631,
            0.5443310539518174,
            0.6804138174397717
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 6
      }
    ]
  }
}