內插法、導數與積分
本節探討內插法和數值微積分的相關數學運算式。
內插法
內插法用於在一組已知的控制點之間建構新的資料點。預測新資料點的能力允許沿著由控制點定義的曲線進行取樣。
以下描述的內插法函式都會傳回一個內插法函式,該函式可以傳遞給其他使用取樣功能的函式。
如果直接傳回,內插法函式會傳回一個陣列,其中包含每個控制點的預測。這在 loess 內插法的情況下非常有用,它首先平滑控制點,然後內插平滑後的點。所有其他內插法函式只會傳回原始控制點,因為內插法會預測通過原始控制點的曲線。
內插法有不同的演算法,它們會產生沿曲線的不同預測。數學運算式庫目前支援以下內插法函式
-
lerp:線性內插法會預測通過每個控制點的點,並在控制點之間形成直線。 -
spline:樣條內插法會預測通過每個控制點的點,並在控制點之間形成平滑曲線。 -
akima:Akima 樣條內插法類似於樣條內插法,但對離群值穩定。 -
loess:Loess 內插法首先執行非線性局部迴歸以平滑原始控制點。然後使用樣條來內插平滑後的控制點。
沿曲線取樣
更好地理解內插法的一種方法是視覺化沿曲線取樣的意義。下面的範例透過在特定的 x 軸範圍之間取樣曲線來放大曲線的特定區域。
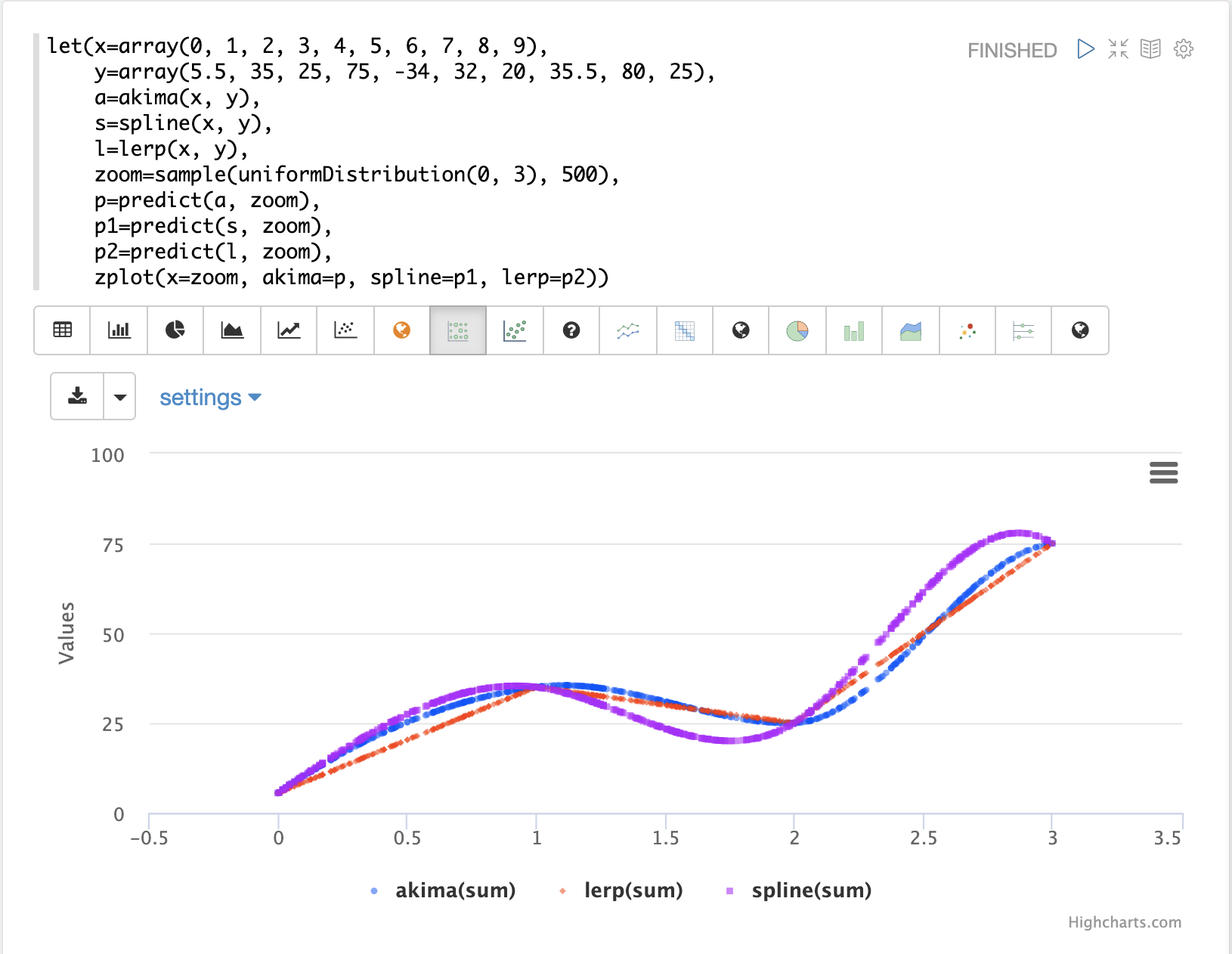
上方的視覺化首先建立兩個陣列,分別包含 x 軸和 y 軸上的點。請注意,x 軸的範圍從 0 到 9。接著,將 akima、spline 和 lerp 函數應用於這些向量,以建立三個內插函數。
然後,從 0 到 3 的均勻分佈中抽取 500 個隨機樣本。這些是新的放大後的 x 軸點,介於 0 和 3 之間。請注意,我們正在對曲線的特定區域進行取樣。
接著,使用 predict 函數來預測取樣 x 軸點的 y 軸點,針對所有三個內插函數。最後,將所有三個預測向量與取樣的 x 軸點一起繪製。
紅線是 lerp 內插,藍線是 akima 內插,紫線是 spline 內插。您可以看到它們在控制點之間產生不同的曲線。
平滑內插
loess 函數是一個平滑內插器,這表示它不會導出通過原始控制點的函數。相反地,loess 函數會返回一個平滑原始控制點的函數。
一種稱為局部迴歸的技術被用於計算平滑曲線。局部迴歸的鄰域大小可以調整,以控制新曲線與原始控制點的符合程度。
loess 函數會傳入 x 軸和 y 軸,並將平滑曲線擬合到資料。如果僅提供單一陣列,則會將其視為 y 軸,並為 x 軸產生一個序列。
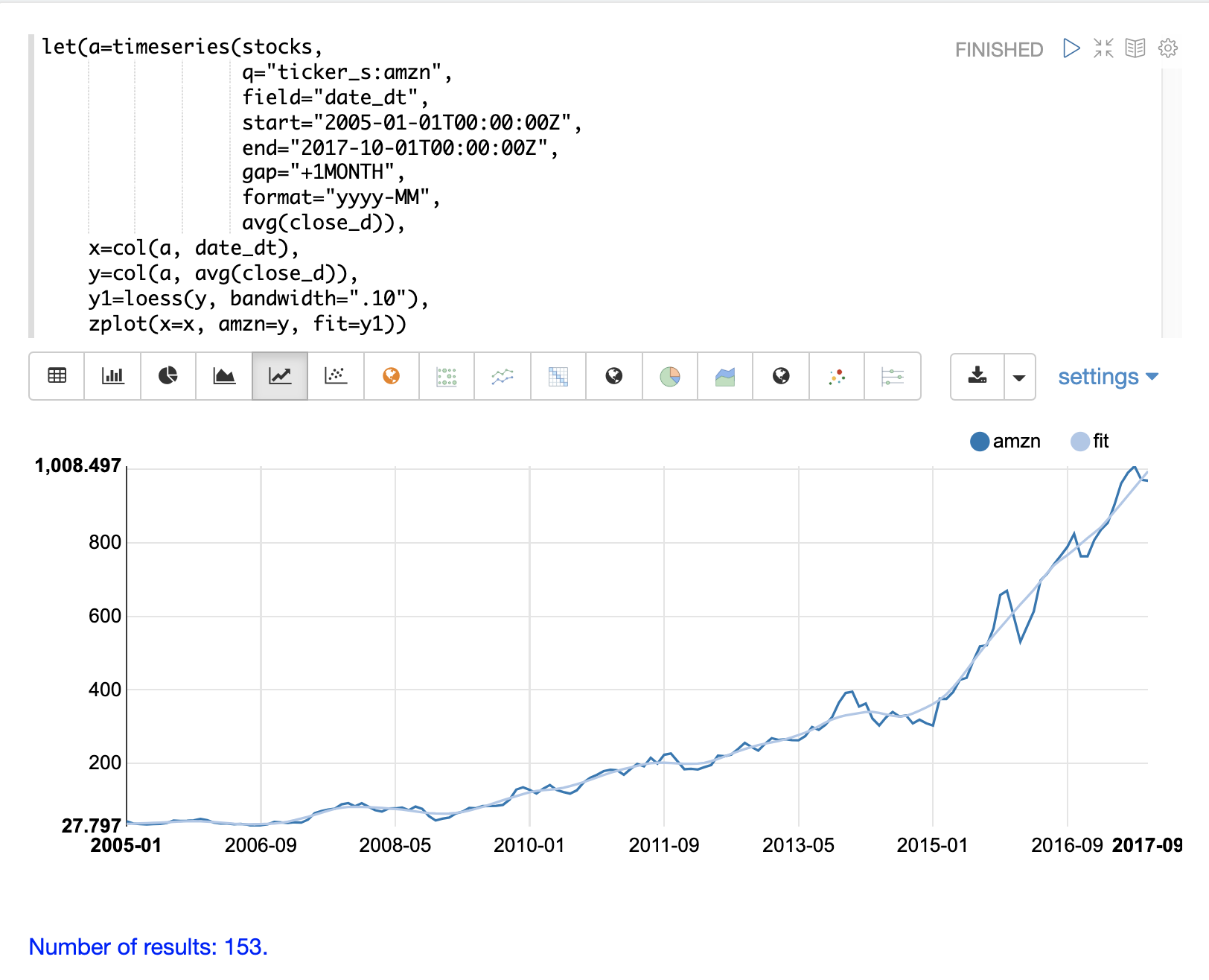
以下範例顯示如何使用 loess 函數來模擬每月時間序列。在這個範例中,使用 timeseries 函數來產生股票代碼 AMZN 的平均收盤價的每月時間序列。然後,將時間序列中的 date_dt 和 avg(close_d) 欄位向量化,並儲存在變數 x 和 y 中。接著,將 loess 函數應用於包含平均收盤價的 y 向量。bandwidth 具名參數指定用於計算局部迴歸的資料集百分比。loess 函數會返回平滑資料點的擬合模型。
然後,使用 zplot 函數來繪製 x、y 和 y1 變數。
導數
函數的導數衡量 y 值相對於 x 值變化率的變化率。
derivative 函數可以計算上述任何內插函數的導數。每個內插函數都會產生與該函數特性相符的不同導數。
一階導數(速度)
一個簡單的範例顯示如何使用 derivative 函數來計算變化率或速度。
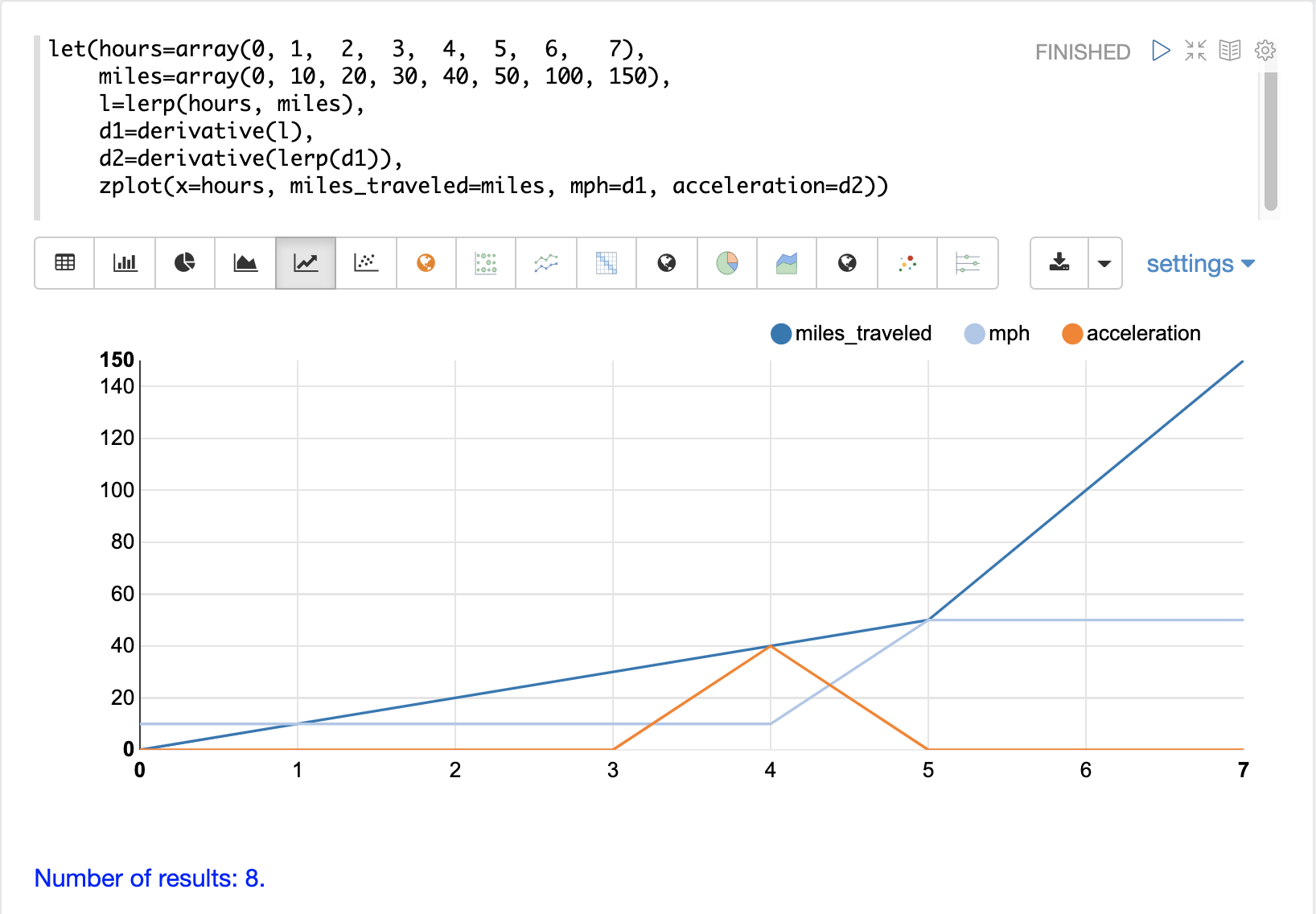
在這個範例中,建立了兩個向量,一個代表小時,另一個代表行駛里程。然後,使用 lerp 函數來建立 hours 和 miles 向量的線性內插。接著,將 derivative 函數應用於線性內插。然後,使用 zplot 繪製 x 軸上的 hours、y 軸上的 miles,以及每個 x 軸點的 mph 作為導數。
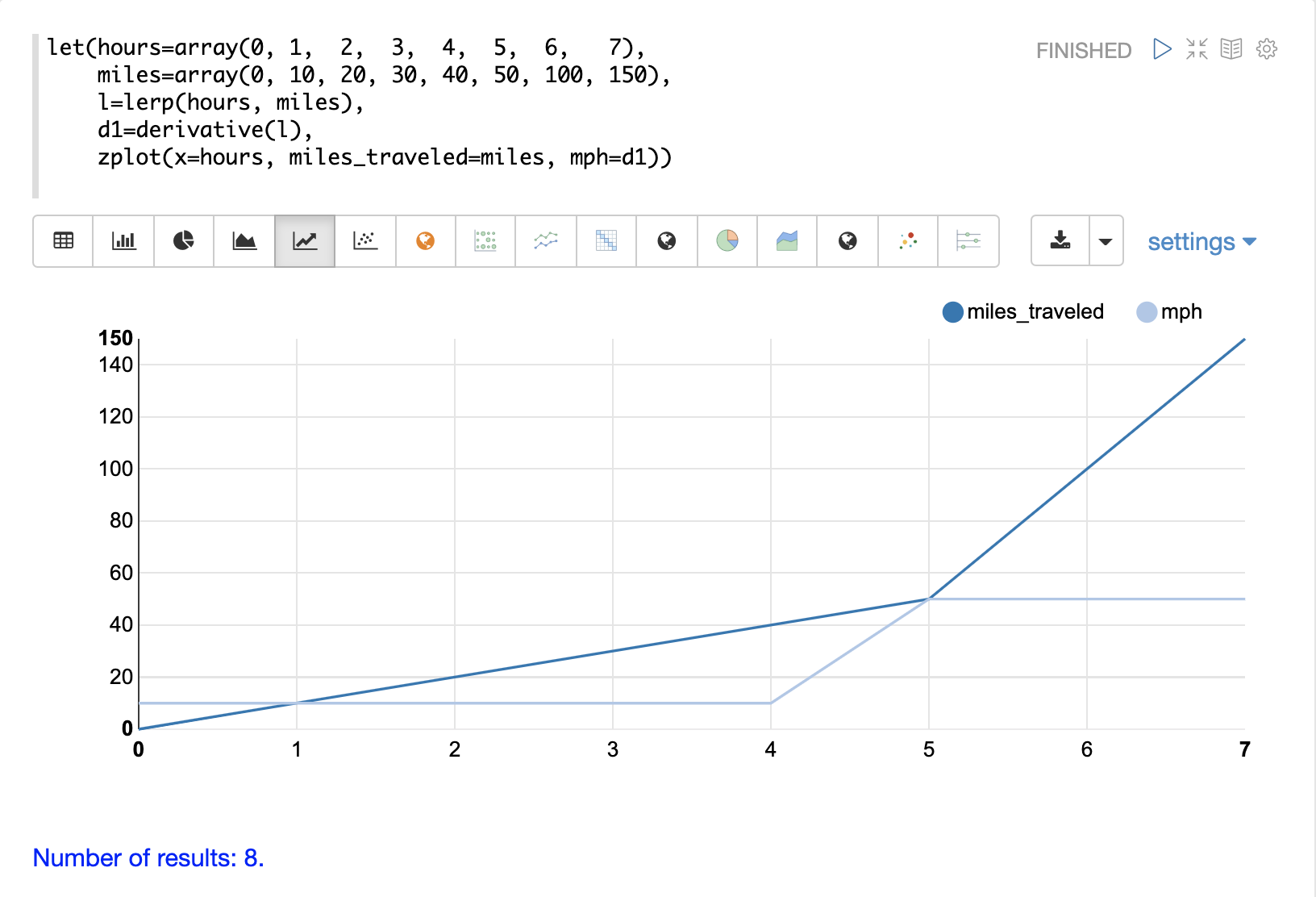
請注意,miles_traveled 線的斜率為 10,直到第 5 小時才變為斜率 50。 mph 線是導數,可視覺化 miles_traveled 線的速度。
另請注意,導數是沿著直線計算的,顯示從一個點到下一個點的立即變化。這是因為線性內插 (lerp) 用作內插函數。如果使用 spline 或 akima 函數,則會產生帶有圓滑曲線的導數。
積分
積分是曲線下方體積的量度。integral 函數計算曲線的累計積分,或內插曲線特定範圍的積分。與 derivative 函數一樣,integral 函數適用於內插函數。
單一積分
如果將 start 和 end 範圍傳遞給 integral 函數,它將計算該特定範圍內曲線下的體積。
在以下範例中,integral 函數會計算曲線的整個範圍(從 0 到 10)的積分。請注意,integral 函數會傳遞內插曲線和起始與結束範圍,並返回該範圍的積分。
let(x=array(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20),
y=array(0, 1, 2, 3, 4, 5.7, 6, 7, 7, 7,6, 7, 7, 7, 6, 5, 5, 3, 2, 1, 0),
curve=loess(x, y, bandwidth=.3),
integral=integral(curve, 0, 10))當此運算式傳送到 /stream 處理常式時,它會回應:
{
"result-set": {
"docs": [
{
"integral": 45.300912584519914
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}累計積分圖
如果將單一內插曲線傳遞給 integral 函數,它會傳回曲線累計積分的向量。累計積分向量包含每個 x 軸點的累計積分計算。累計積分是透過取每個 x 軸點與第一個 x 軸點之間的範圍的積分來計算的。在上述範例中,這表示要計算如下的積分向量:
let(x=array(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20),
y=array(0, 1, 2, 3, 4, 5.7, 6, 7, 7, 7,6, 7, 7, 7, 6, 5, 5, 3, 2, 1, 0),
curve=loess(x, y, bandwidth=.3),
integrals=array(0, integral(curve, 0, 1), integral(curve, 0, 2), integral(curve, 0, 3), ...)累計積分的圖表可視覺化曲線的累計體積在每個點 x 軸點下方的量。
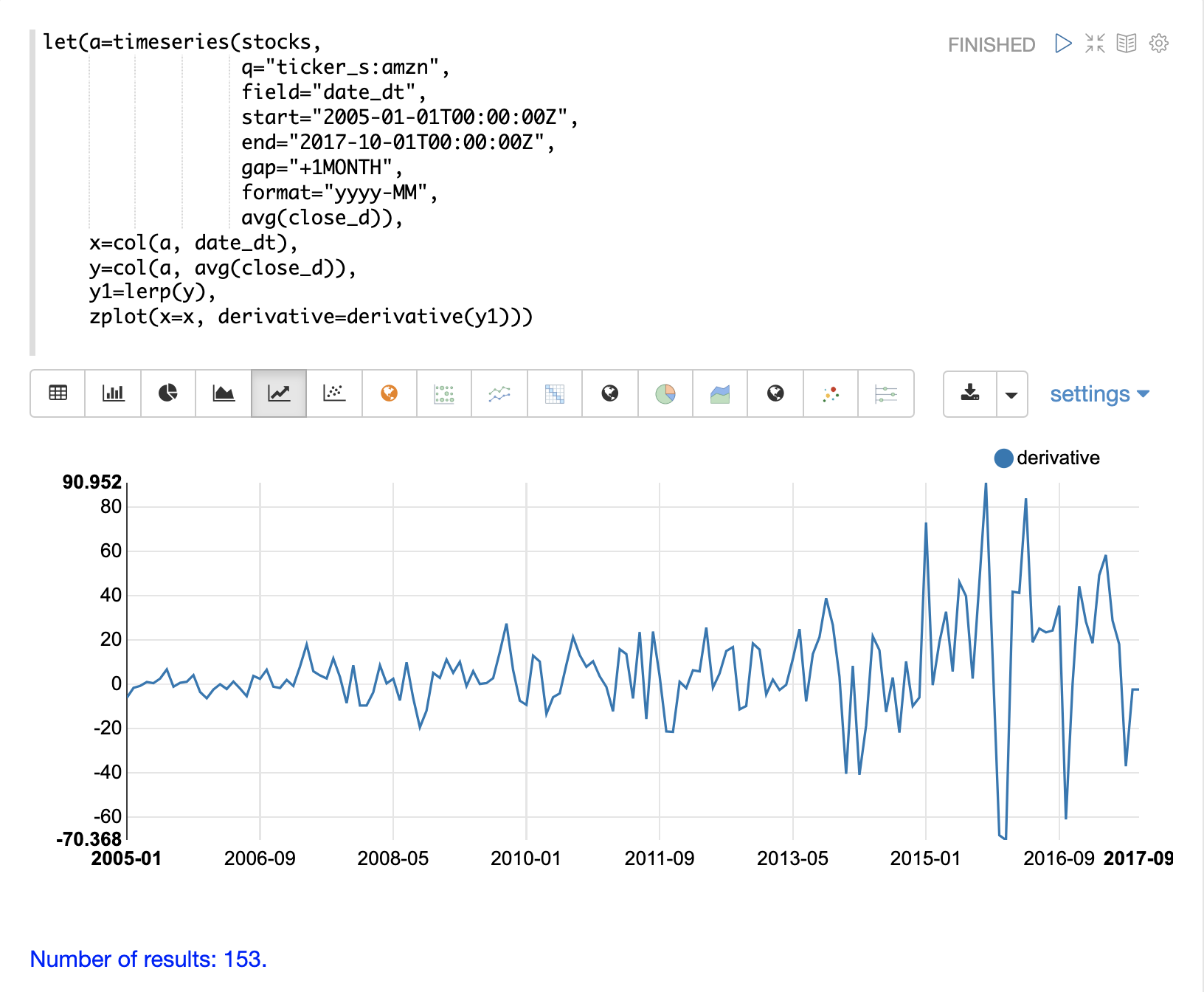
以下範例顯示由 timeseries 函數產生的時間序列的累計積分圖。在這個範例中,會針對股票代碼 amzn 的平均收盤價產生每月時間序列。使用 spline 將 avg(close) 欄位向量化並內插。
然後,使用 zplot 函數來繪製時間序列的累計積分。
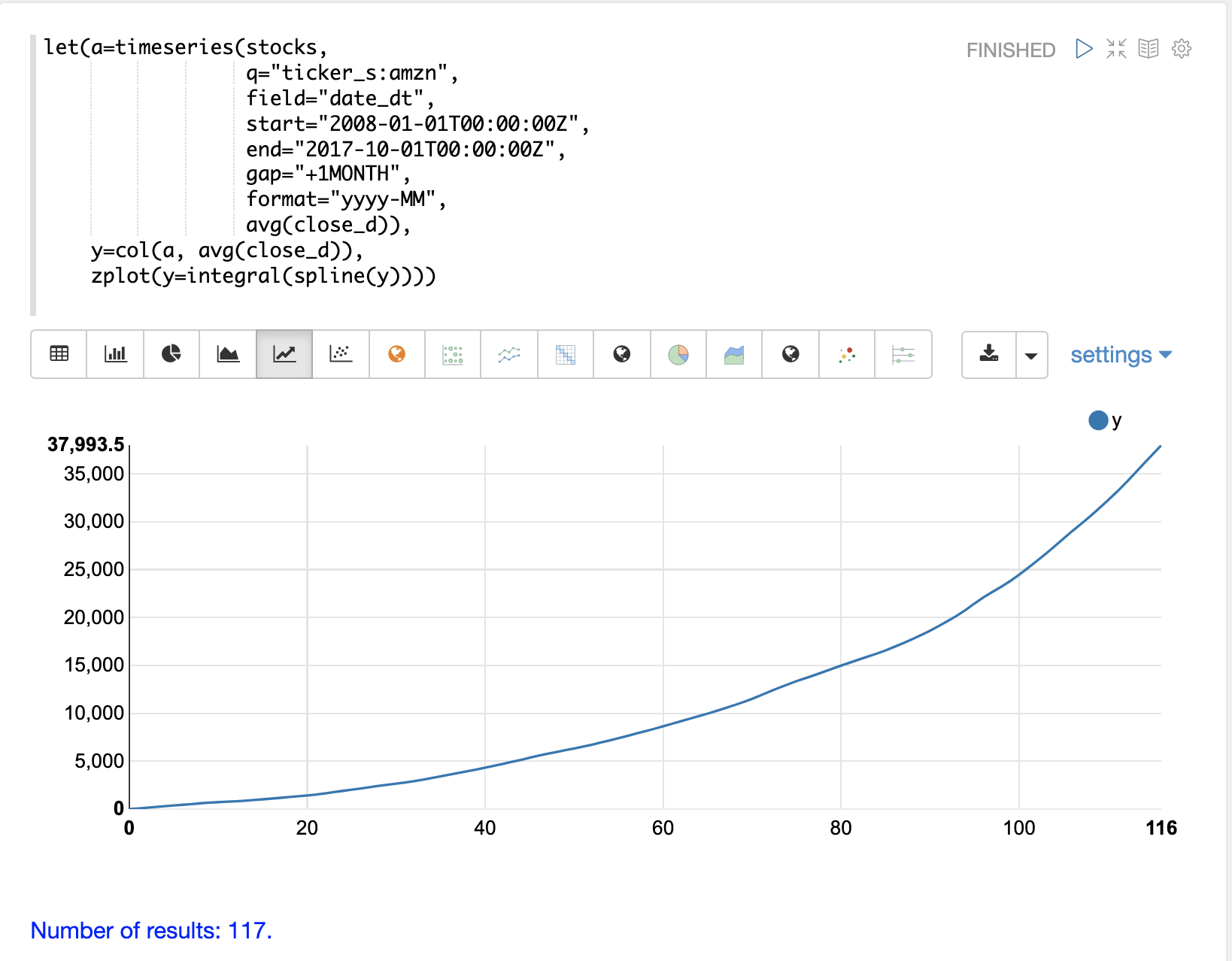
上方的圖表可視覺化隨著 AMZN 股價隨時間變化的曲線下的體積。由於此圖是累計的,因此股價隨時間保持不變的股價時間序列,將具有正線性斜率。股價上漲的股票將具有凹形,而股價下跌的股票將具有凸形。
在此特定範例中,積分圖隨著時間推移變得更加凹,顯示股價加速上漲。
雙三次樣條
bicubicSpline 函數可用於內插和預測資料網格中任何位置的值。
一個簡單的範例將使這一點更加清楚
let(years=array(1998, 2000, 2002, 2004, 2006),
floors=array(1, 5, 9, 13, 17, 19),
prices = matrix(array(300000, 320000, 330000, 350000, 360000, 370000),
array(320000, 330000, 340000, 350000, 365000, 380000),
array(400000, 410000, 415000, 425000, 430000, 440000),
array(410000, 420000, 425000, 435000, 445000, 450000),
array(420000, 430000, 435000, 445000, 450000, 470000)),
bspline=bicubicSpline(years, floors, prices),
prediction=predict(bspline, 2003, 8))在此範例中,使用雙三次樣條來內插房地產資料矩陣。矩陣的每一列都代表特定的年份。矩陣的每一欄都代表建築物的樓層。數字網格是每年和樓層的公寓平均售價。例如,在 2002 年,9 樓的平均售價為 415000(第 3 列,第 3 欄)。
然後,使用 bicubicSpline 函數來內插網格,並使用 predict 函數來預測 2003 年 8 樓的值。請注意,矩陣不包含 2003 年 8 樓的資料點。bicubicSpline 函數會根據矩陣中的周圍資料建立該資料點。
{
"result-set": {
"docs": [
{
"prediction": 418279.5009328358
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}